ALU - Sčítačka/odčítačka
Sčítačka je podstatná část ALU. Po určitých úpravách z ní můžeme udělat dokonce i odčítačku. Začneme jednoduše, a to s jedno bitovou verzí.
Half-adder (1 bit adder)
Pravdivostní tabulka pro half-adder vypadá následovně.
| A | B | OUT | COUT |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Pomocí karnaughovy mapy nebo i logiky (odkoukání) můžeme zjistit, že sčítání (OUT) je vlastně XOR a COUT je jenom AND. Takže half-adder vypadá následovně.
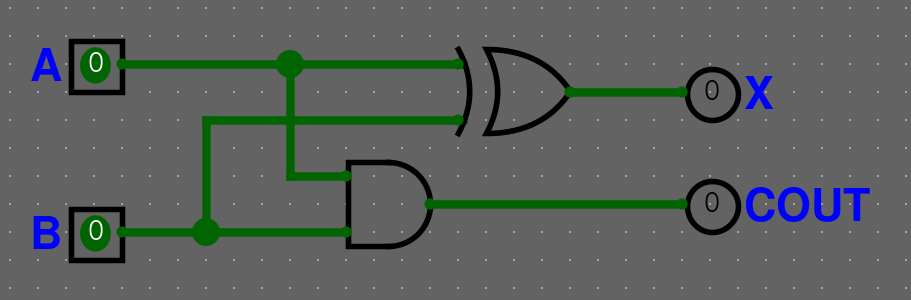
Full-adder
Full-adder využívá half adder a pomocí něj přijímá další argument a to CIN, neboli carry in.
Pravdivostní tabulka pro full-adder vypadá následovně.
| CIN | A | B | OUT | COUT |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
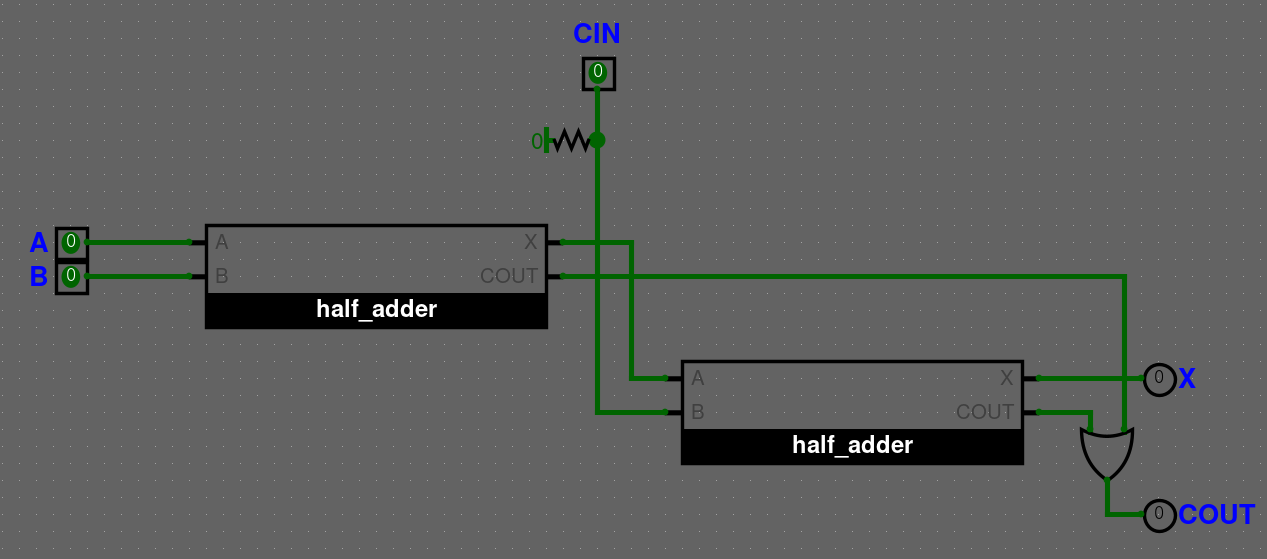
Jediné, co tedy uděláme je, že přidáme half-adder 2 krát, jeden na A+B a druhý na výsledek z prvního X a CIN, neboli X+CIN.
COUT half-adderů by se měly sčítat, ale jelikož nemůže nastat případ, kdy jsou oba dva COUT 1, tak nám stačí OR. Taky se nemusíme bát přetečení, jelikož při sčítání 3 bitů se hodnota vždy vejde do 2 bitů (maximální hodnota je 3).
Odčítačka
Pro pochopení odčítačky si musíme říct, co jsou to záporná čísla. Záporná čísla můžeme v binárce vyjadřovat mnoho způsoby, ale nejčastější je dvojkový doplněk.
Dvojkový doplněk (two's complement)
Když pracujeme s n-bitovými čísly, tak pracujeme s tělesem \(Z_{2^n}^+\). Chceme vytvořit taková pravidla, že budeme moct pomocí sčítání odčítat.
- Pro každé kladné \(b^+\) musí existovat takové \(b^-\), aby platitlo \(a-b^+ = a + (-b^+) = a + b^-\).
- Taky musí platit \(b^+ + b^- = 0\)
Potřebujeme tedy najít aditivní inverzi
\(b^- = 2^n - b^+ = (2^n - 1) - b^+ + 1\)
\((2^n - 1)\) je řetězec samých jedniček a odečtením od takové hodnoty nikdy nenastane žádný přenos a odečtená hodnota se touto operací jednoduše zneguje. Dostáváme tedy pravidlo pro výpočet opačného čísla a to: \(b^- = \overline{b^+} + 1\)
Rozdělíme tak těleso na dvě poloviny na zápornou a nezápornou. Viz. obrázek

Zkráceně dvojkový doplněk spočívá ve vyhrazení prvního bitu pro znaménko. 1 znamená - a 0 znamená + s tím, že jsou u negativních čísel znegované bity a poté přičtena 1. Pochopíte z následného příkladu.
| Dvojková soustava | Decimální soustava |
|---|---|
000 | 0 |
001 | 1 |
010 | 2 |
011 | 3 |
100 | -4 |
101 | -3 |
110 | -2 |
111 | -1 |
Jeho hlavní výhoda spočívá v odčítání, jelikož pomocí tohoto znázornění platí následující: \(A-B = A + \overline{B} + 1\)
Tuto funkcionalitu tedy neimplementujeme nějak zvlášť, ale pomocí sčítačky, kde nastavíme CIN na 1 a znegujeme vstup B.