Booleova algebra

Booleova algebra je algebraická struktura se dvěma binárními a jednou unární operací.

Jedná se o šestici (\(A\), \(\land\), \(\lor\), \(-\), \(0\), \(1\)), kde \(A\) je neprázdná množina

Nejmenší prvek \(0 \in A\)
Největší prvek \(1\in A\)
Unární operace (negace) \(\overline{0} = 1\)

Budeme se soustředit na dvouprvkovou Booleovu algebru tj. budou 2 prvky:

\(1\) - (\(true\))
\(0\) - (\(false\))

Základní matematické symboly

Název	Znak	Definice
Negace	\(\neg\) nebo \(\overline{x}\)	Neguje vstup, tedy z 1 dostaneme 0 a obráceně
Disjunkce (spojení)	\(\lor\) nebo \(+\)	Logické nebo
Konjunkce (průsek)	\(\land\) nebo \(\cdot\)	Logické a

Axiomy

Název	Součet	Součin
komutativní	\(x+y=y+x\)	\(x{\cdot}y=y{\cdot}x\)
distrubutivní	\((x+y){\cdot}z=x{\cdot}z+y{\cdot}z\)	\((x \cdot y)+z=(x+z){\cdot}(y+z)\)
neutralita 0 a 1	\(x+0=x\)	\(x{\cdot}1=x\)
agresivita 0 a 1	\(x+1=1\)	\(x{\cdot}0=0\)
vyloučení třetího	\(x+\overline{x} = 1\)	\(x{\cdot}\overline{x} = 0\)

Prohozením \(0 \leftrightharpoons 1\) a zároveň \(+ \leftrightharpoons \cdot\) v celém obvodu/výrazu zůstane chování (logická funkce) zachovaná (samozřejmě při prohození 1 a 0 i na vstupech/výstupech). Toto chování vychází ze symetrie námi vybraných operátorů \(+\) a \(\cdot\) k modelování Booleovy algebry.

Výraz	Duální výraz
\(x \cdot \overline{y + \overline{z}}\)	\(\overline{\overline{x} + \overline{\overline{y} \cdot \overline{\overline{z}}}}\)

De Morganovy zákony

Zákon
\(\overline{x} + \overline{y} = \overline{(x{\cdot}y)}\)
\(\overline{x} {\cdot} \overline{y} = \overline{(x+y)}\)

Zákon je efektivně lokální aplikací duality Booleovy algebry. Pokud v nějaké sekci obvodu vyměníme \(+\) (OR) za \(\cdot\) (AND) a obráceně, a na rozhraní sekce všechny znegujeme všechny signály (tím uvnitř sekce vyměníme 1 a 0), tak chování celého obvodu zůstane zachováno.
Z toho vyplývá, že lze vytvořit verzi De Morganových zákonů i pro 3 a více vstupů, klidně s odlišnými operátory.

Užitečné zákony

Název	Součet	Součin
asociativní	\(x+(y+z)=(x+y)+z\)	\(x{\cdot}(y{\cdot}z)=(x{\cdot}y){\cdot}z\)
o idempotenci prvků (absorbce)	\(x+x=x\)	\(x{\cdot}x=x\)
absorbce	\(x+x{\cdot}y=x\)	\(x{\cdot}(x+y)=x\)
dvojí negace	\(\overline{\overline{{x}}} = x\)	\(\overline{\overline{{x}}} = x\)

Hradlo XOR

Hradlo XOR můžeme kdykoliv zaměnit za disjunktivní normální formu (DNF) jeho logické funkce:

\(x \oplus y = x \cdot \overline{y} + \overline{x} \cdot y\)

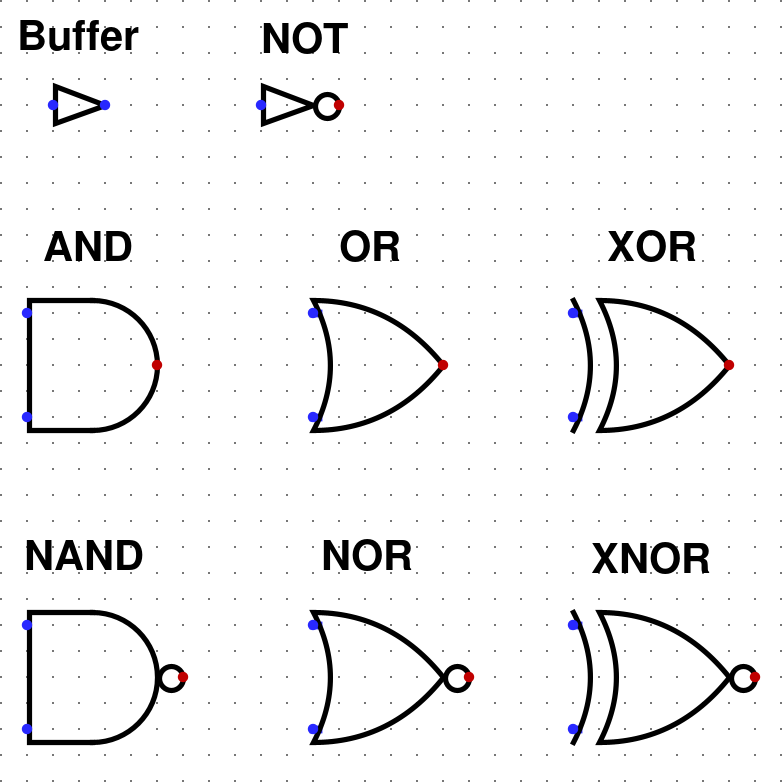
Hradla - Teorie

Obsah:

Pravdivostní tabulka

Pro značení budeme používat pravdivostní tabulku, která označuje nějaký vztah mezi vstupy a výstupy. Jedná se o jednoduchou tabulku, kde se nachází libovolně vstupů, (typicky A,B,CIN,...) a výstupů (typicky X,COUT,OUT,...). S následujících příkladů u hradel, hned pochopíte o co jde.

Hradla s jedním vstupem

Hradla, které mají jeden vstup jsou následující

Buffer (repeater)
NOT

Buffer (repeater)

Buffer se převážně využívá na zopakování a posílení vstupu. Taky tím "ukazujete", jakým směrem teče proud.

Symbol

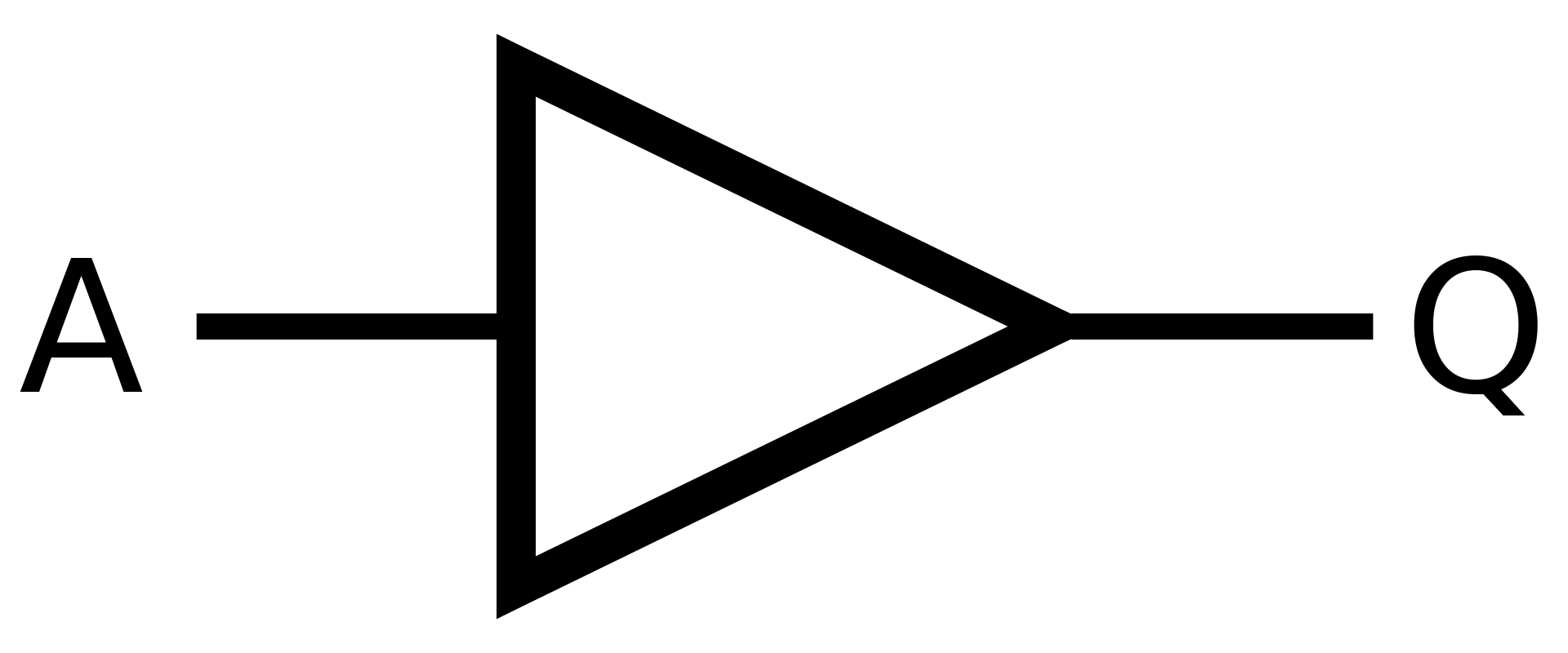
Definice

Matematická definice

\(Q = A\)

Zápis v C

bool A;
bool Q = A;

Pravdivostní tabulka

A	Q
0	0
1	1

NOT

Hradlo NOT použijete, když potřebujete změnit hodnotu na její opak.

Neboli 0 → 1 nebo 1 → 0

Symbol

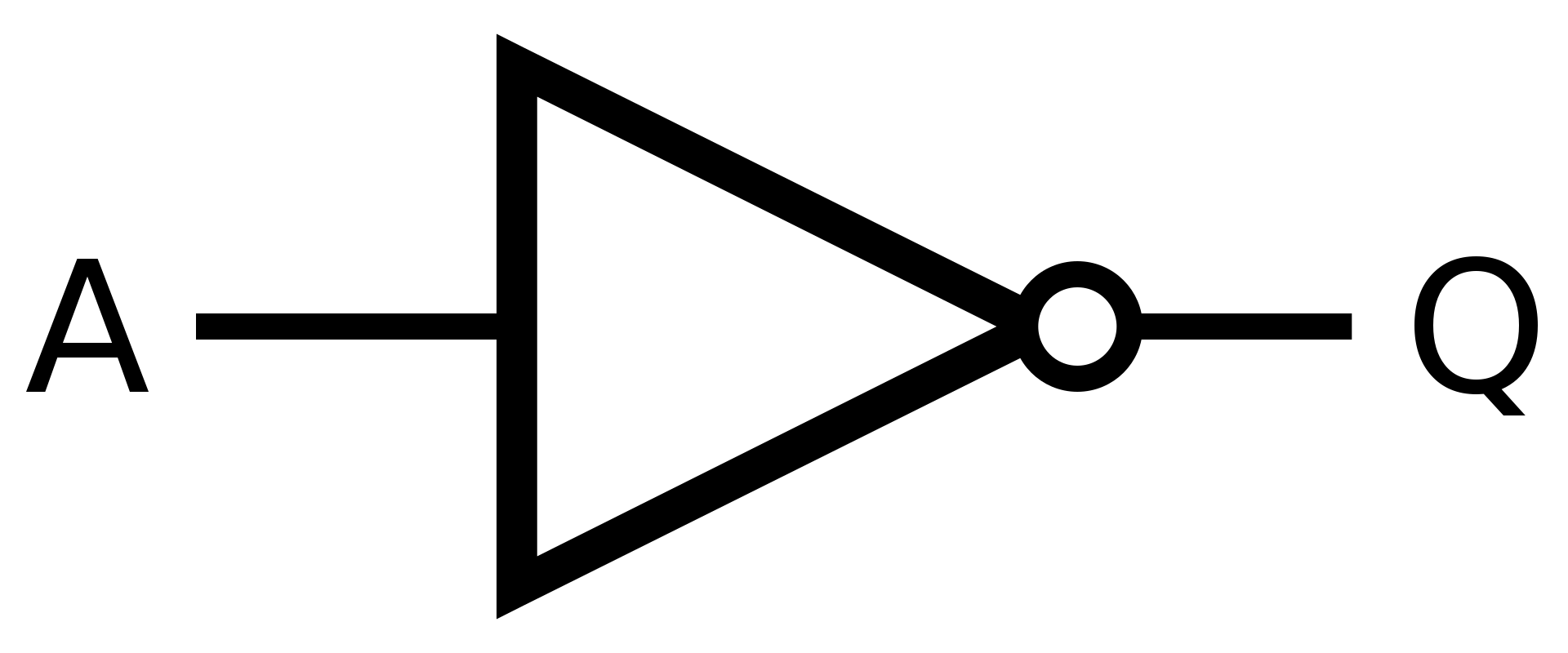
Definice

Matematická definice

\(Q = \overline{A}\)

Zápis v C

bool A;
bool Q = !A;

Pravdivostní tabulka

A	Q
0	1
1	0

Základní hradla se dvěma vstupy

Základní hradla, které mají dva vstupy jsou následující

AND

Hradlo AND neboli logické "a" , se využívá když chcete naplnit dvě podmíky.

Pokud platí A a B, tak pošli na výstup hodnotu 1

Symbol

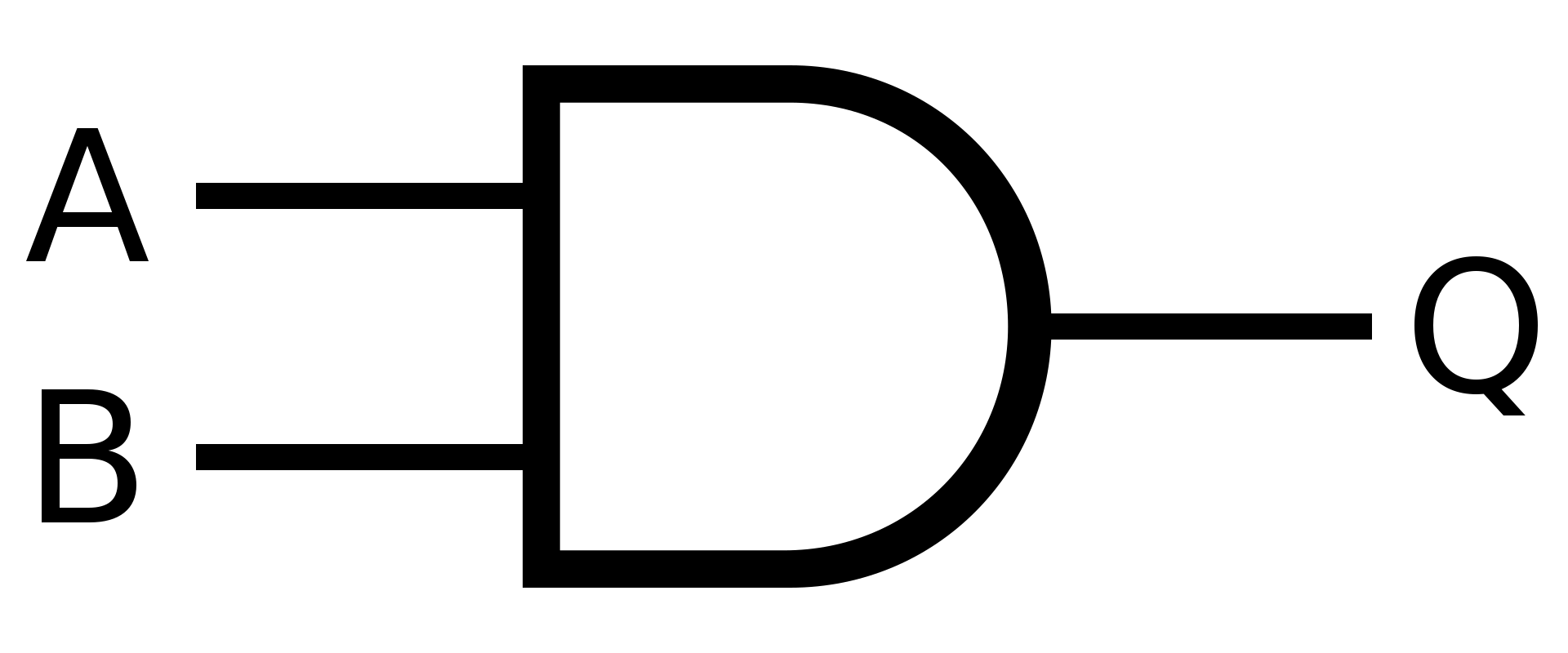
Definice

V Booleově algebře se hradlo AND rovná násobení

\(Q = A \cdot B\)

Zápis v C:

bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A && B;

Pravdivostní tabulka

A	B	Q
0	0	0
0	1	0
1	0	0
1	1	1

OR

Hradlo OR neboli logické "nebo" , se využívá když chcete naplnit aspoň jednu podmíku.

Pokud platí A nebo B, tak pošli na výstup hodnotu 1

Symbol

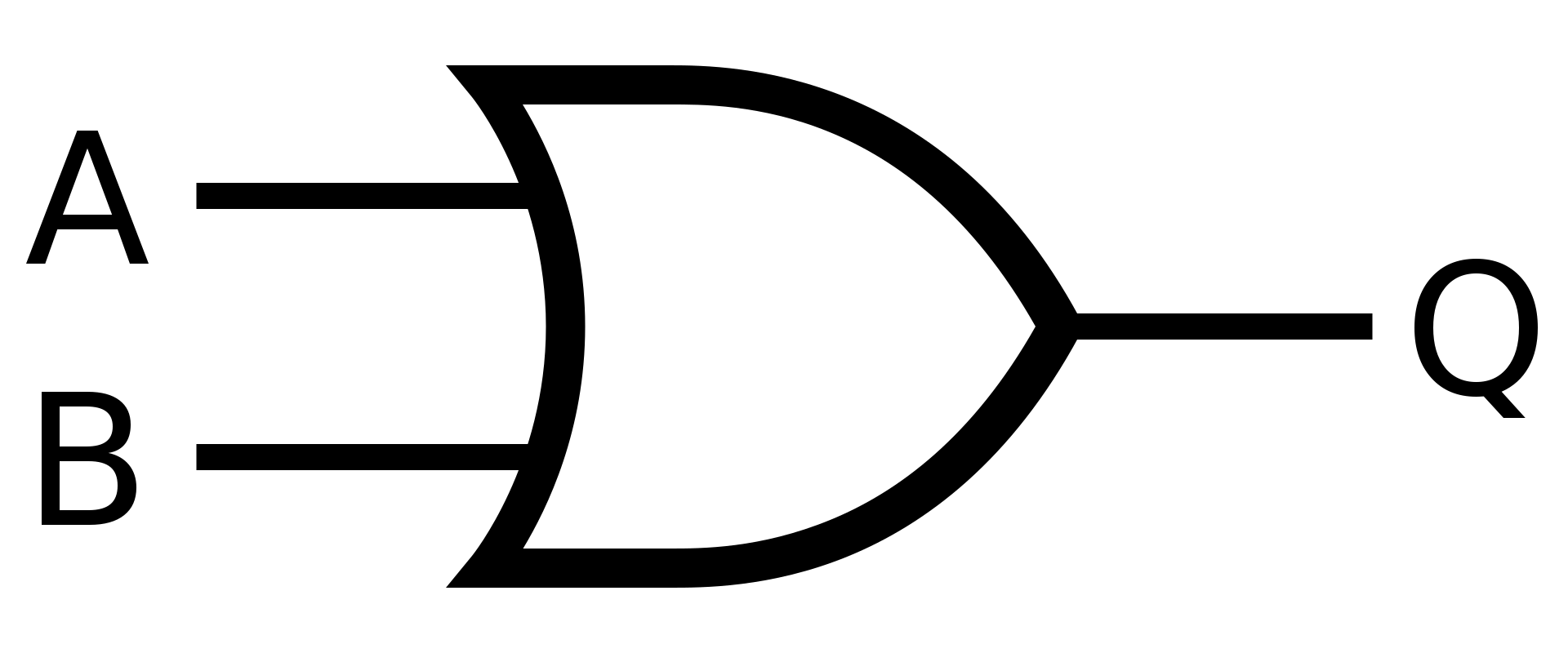
Definice

V Booleově algebře se hradlo OR rovná součtu

\(Q = A + B\)

Zápis v C:

bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A || B;

Pravdivostní tabulka

A	B	Q
0	0	0
0	1	1
1	0	1
1	1	1

XOR

Hradlo XOR neboli exkluzivní OR , se využívá když chcete naplnit pouze jednu podmíku. Jednoduše řečeno, když se sobě nerovnají.

*Pokud platí právě A nebo právě B, tak pošli na výstup hodnotu 1 ... Pokud se A nerovná B

Symbol

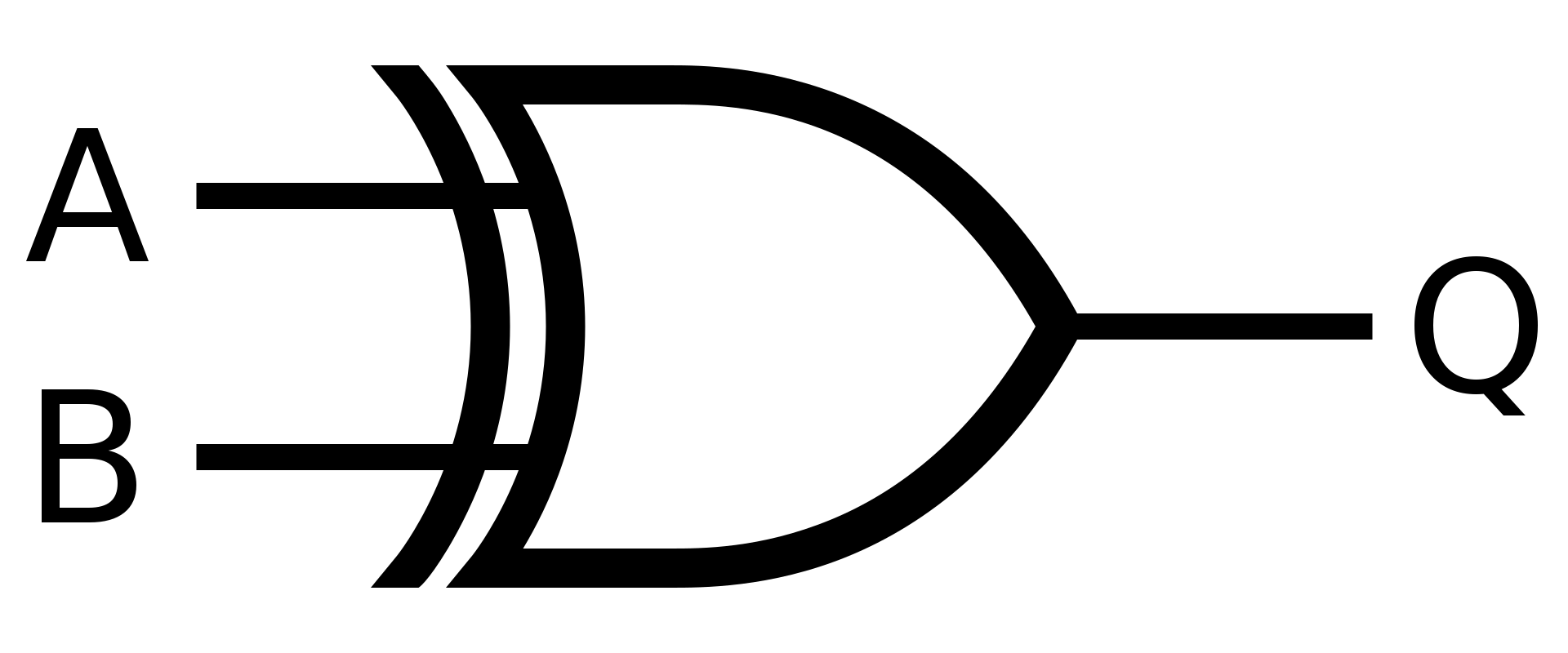
Definice

V Booleově algebře se pro hradlo XOR používá symbol \(\bigoplus\)

\(Q = A \bigoplus B\)

Zápis v C

bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A ^ B;

Pravdivostní tabulka

A	B	Q
0	0	0
0	1	1
1	0	1
1	1	0

Opaky základních hradel se dvěma vstupy

Opaky základních hradel, existují právě 3

NAND (opak AND)
NOR (opak OR)
XNOR (opak XOR)

NAND

Hradlo NAND má opačný výstup hradla AND

Pokud neplatí A a B, tak pošli na výstup hodnotu 1

Symbol

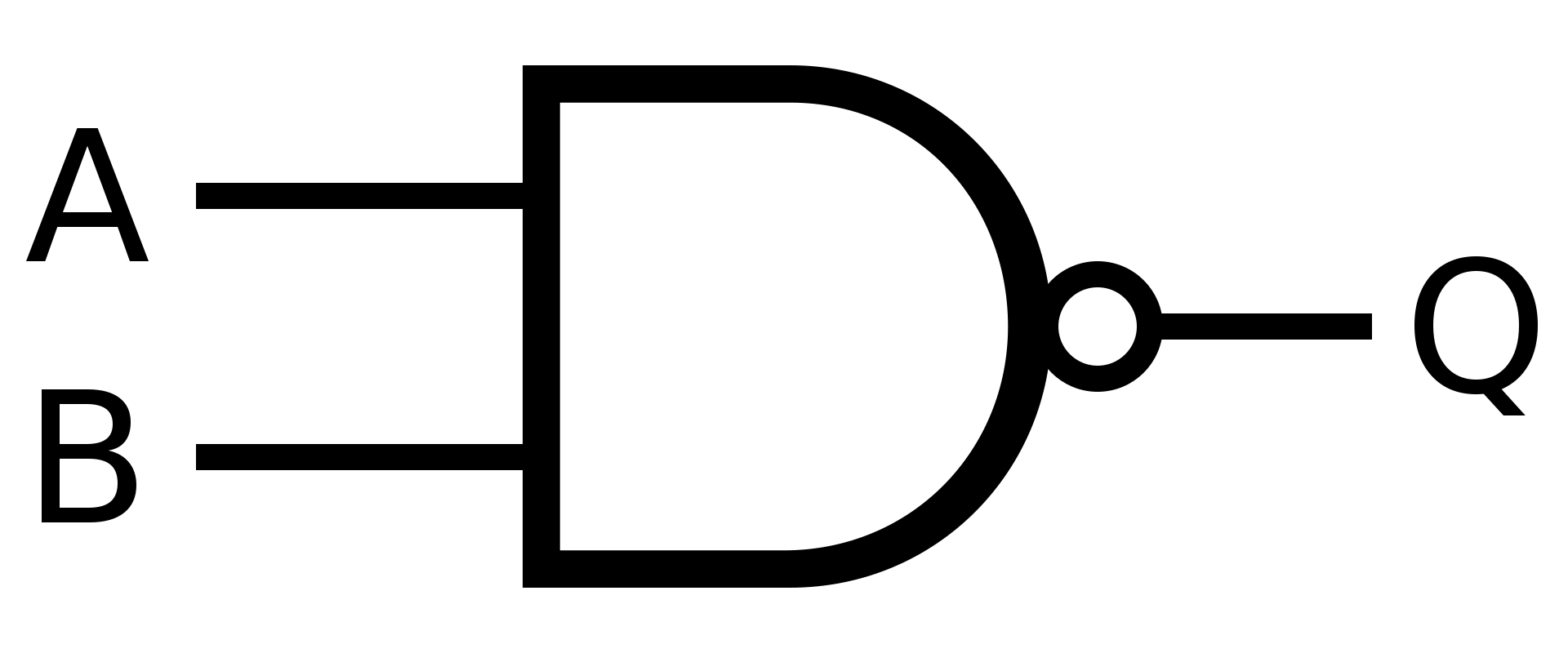
Definice

V Booleově algebře se hradlo NAND rovná negaci násobení

\(Q = \overline{(A \cdot B)}\)

Zápis v C:

bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A && B);

Pravdivostní tabulka

A	B	Q
0	0	1
0	1	1
1	0	1
1	1	0

NOR

Hradlo NOR má opačný vstup hradla OR

Pokud neplatí A nebo B, tak pošli na výstup hodnotu 1

Symbol

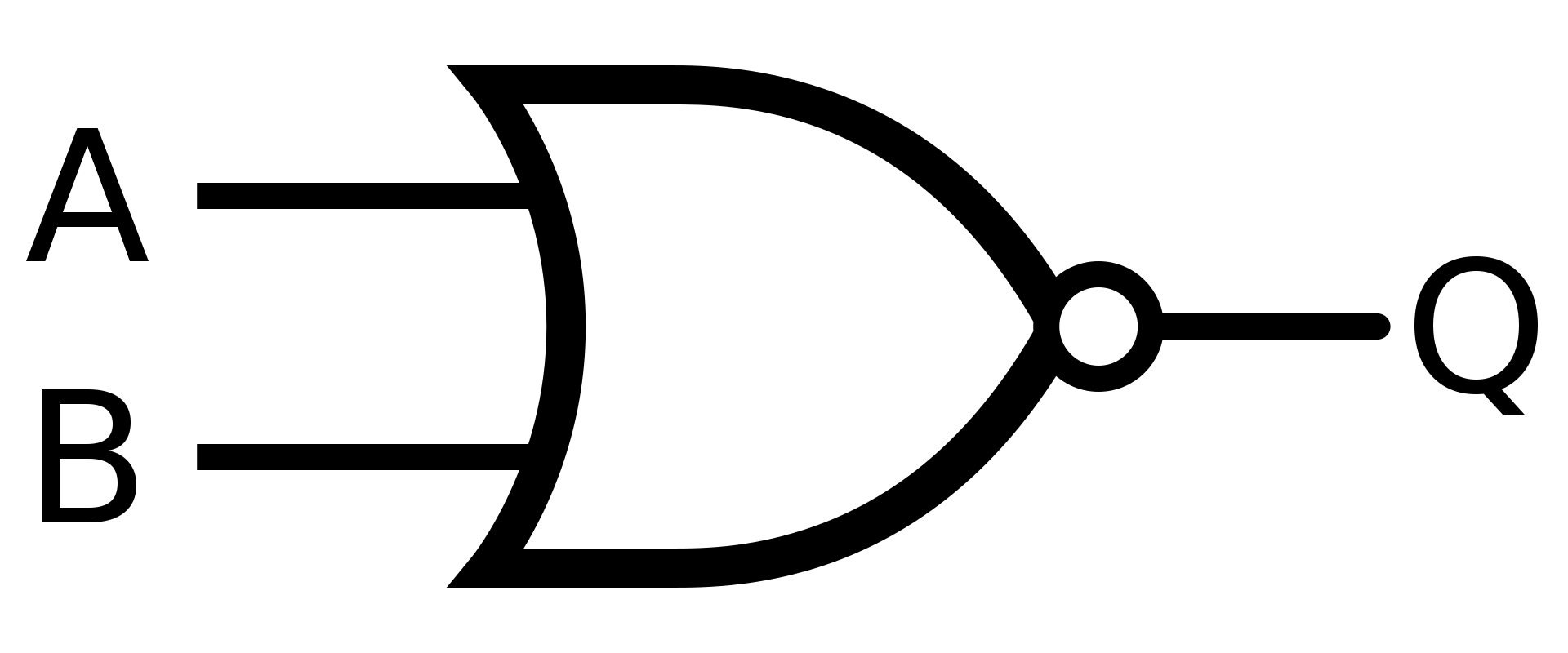
Definice

V Booleově algebře se hradlo NOR rovná negaci součtu

\(Q = \overline{(A + B)}\)

Zápis v C:

bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A || B);

Pravdivostní tabulka

A	B	Q
0	0	1
0	1	0
1	0	0
1	1	0

XNOR

Hradlo XNOR je opak hradla XOR, jednoduše řečeno se jedná o ekvivalenci

Pokud se A rovná B

Symbol

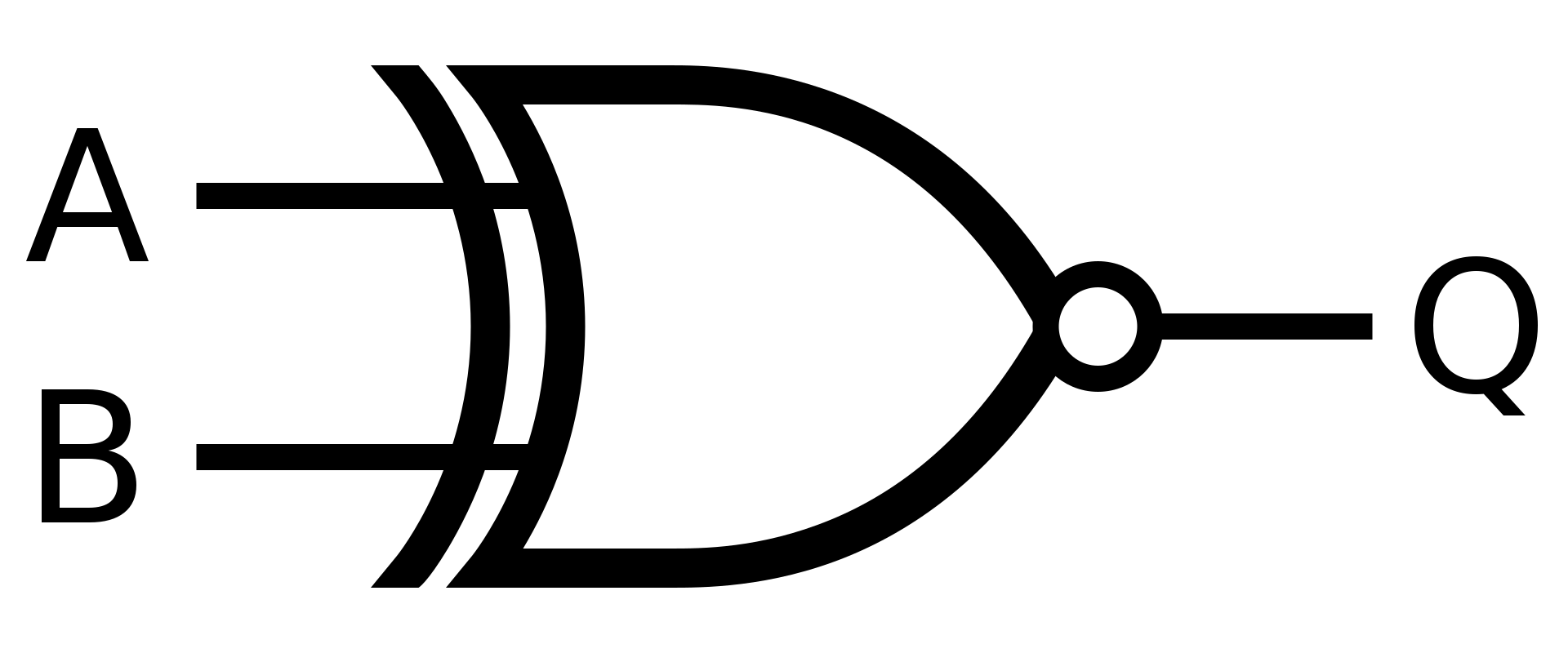
Definice

V Booleově algebře se hradlo XNOR rovná negaci operaci ((\bigoplus))

\(Q = \overline{(A \bigoplus B)}\)

Zápis v C:

bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A ^ B);

Pravdivostní tabulka

A	B	Q
0	0	1
0	1	0
1	0	0
1	1	1

Cheat sheet

Cheat sheet pro logické brány

Vstup A a Vstup B dává výstup <operace>

A	B	AND	OR	XOR	NAND	NOR	XNOR
0	0	0	0	0	1	1	1
0	1	0	1	1	1	1	0
1	0	0	1	1	1	1	0
1	1	1	1	0	0	0	1

Zobrazení logických bran v logisimu

Karnaughova mapa

Karnaughova mapa je prostředek pro minimalizaci logických obvodů. Pro pochopení Karnaughovy mapy musíme první pochopit Grayův kód.

Grayův kód

Grayův kód je binární číselná soustava, ve které se každé dvě po sobě jdoucí hodnoty liší v jedné bitové pozici.

Příkladná tabulka pro 3 bity (tučně zvýrazněný změněný bit):

A	B	C
0	0	0
0	0	1
0	1	1
0	1	0
1	1	0
1	1	1
1	0	1
1	0	0

Karnaughova mapa - příklad 1

Máme pravdivostní tabulku se vstupy \(A,B,C,D\) a výstupem \(Q\):

A	B	C	D	Q	index bitu
0	0	0	0	0	0
0	0	0	1	1	1
0	0	1	0	1	2
0	0	1	1	1	3
0	1	0	0	0	4
0	1	0	1	0	5
0	1	1	0	0	6
0	1	1	1	0	7
1	0	0	0	1	8
1	0	0	1	1	9
1	0	1	0	1	10
1	0	1	1	1	11
1	1	0	0	1	12
1	1	0	1	1	13
1	1	1	0	0	14
1	1	1	1	0	15

Vytvoříme tabulku pomocí indexů v pravdivostní tabulce (odvíjí se od Grayova kódu). Neboli doplníme do obrázku

Vznikne nám následující tabulka

Zakroužkujeme sousedy

Musíme zakroužkovat všechny \(1\), kroužkujeme buď samostatnou \(1\) (v tomto případě je výsledek stejný jako při stavění pomocí mintermů přímo z pravdivostní tabulky, tady K-mapa nemá žádný přínos) nebo obdélníky s obsahem rovným některé mocnině \(2\) \(2,4,8...\), z čehož přímo výplývá (jako nutná podmínka), že obě dělky stran obdélníků musí být mocniny dvou.

Vytvoříme výrazy

Růžová - \(A \cdot \overline{C}\)
Zelená - \(A \cdot \overline{B}\)
Modrá - \(\overline{B} \cdot C\)
Oranžová - \(\overline{A} \cdot \overline{B} \cdot \overline{C} \cdot D\)

Sečteme výrazy

\((A \cdot \overline{C}) + (A \cdot \overline{B}) + (\overline{B} \cdot C ) + (\overline{A} \cdot \overline{B} \cdot \overline{C} \cdot D)\)

Upravíme výraz

\(A\overline{C}+A\overline{B}+\overline{B}C+\overline{A} \cdot \overline{B} \cdot \overline{C} \cdot D = A\overline{C} + \overline{B} \cdot (A + C + \overline{A} \cdot \overline{C} \cdot D)\)

Karnaughova mapa - příklad 2

Máme pravdivostní tabulku se vstupy \(A,B,C\) a výstupem \(Q\):

A	B	C	Q
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	0

Vytvoříme si Karnaughovu mapu (tam kde jsou písmena, tak je hodnota nastavená na 1)

Doplníme do tabulky

Zakroužkujeme největší obdelníky a vyjádříme je

POZOR: oranžový 1x1 obdélník není optimální (maximální), lepší by byl jako 2x2 čtverec přecházející přes hranu. Je to takhle zvolen abychom ukázali, že K-Mapa dál funguje, jenom není výsledek optimální - 1x1 čtverec je potřeba vyjádřit jako 4-term, místo 2-termu pokud bychom udělali 2x2.

Vidíme, že je blok nezávislý na tom, jestli je \(A\) \(0\) nebo \(1\) , takže zahrneme jen proměnou \(B\) a \(C\)

\(B\) musí být \(0\)
\(C\) musí být \(0\)

\(Q_1 = \overline{B} * \overline{C}\)

Součin jsme použili, protože je \(*\) totožné logickému a zároveň platí (v programovacím jazyku C -->&&)

Jelikož se jedná o torus (viz. gif), můžeme označit i hodnoty, které se nacházejí "vedle sebe" (na začátku a na konci)

Vidíme, že je výraz \(Q_2\) nezávislý na proměnné \(B\) (může být \(0\) nebo \(1\))

\(A\) musí být \(0\)
\(C\) musí být \(0\)

\(Q_2 = \overline{A} * \overline{C}\)

Sjednotíme výrazy

Výsledné výrazy sečteme

\(Q = Q_1 + Q_2 = (\overline{B} * \overline{C}) + (\overline{A} * \overline{C})\)

Výsledný výraz si můžeme postavit v logisimu viz. obrázek

Zkontrolujeme pravdivostní tabulku.
1. Klikneme pravým tlačítkem na circuit v nabídce (základní je main)
2. Klikneme na tlačítko Build Circuit
3. Potvrdíme tlačítkem OK, popřípadě Yes
4. Vybereme v nabídce Table
5. Dostaneme tabulku viz. obrázek

Teorie - Příprava na test

1. Nakresli logická hradla, zapiš operátor hradla jako výraz (např. X=A+B), nakresli pravdivostní tabulku:

a) NOT

Řešení - symbol

Řešení

\(X = \overline{A}\)

A	X
0	1
1	0

b) OR

Řešení - symbol

Řešení

\(X = A + B\)

A	B	X
0	0	0
0	1	1
1	0	1
1	1	1

c) XNOR

Řešení - symbol

Řešení

\(X = \overline{(A \bigoplus B)}\)

A	B	X
0	0	1
0	1	0
1	0	0
1	1	1

d) AND

Řešení - symbol

Řešení

\(X = A \cdot B\)

A	B	X
0	0	0
0	1	0
1	0	0
1	1	1

2. Pojmenuj následující hradla, zapiš jejich výraz a pravdivostní tabulku

Řešení

NOR

\(X = \overline{(A + B)}\)

A	B	X
0	0	1
0	1	0
1	0	0
1	1	0

Řešení

XOR

\(X = A \bigoplus B\)

A	B	X
0	0	0
0	1	1
1	0	1
1	1	0

Řešení

NAND

\(X = \overline{(A \cdot B)}\)

A	B	Q
0	0	1
0	1	1
1	0	1
1	1	0

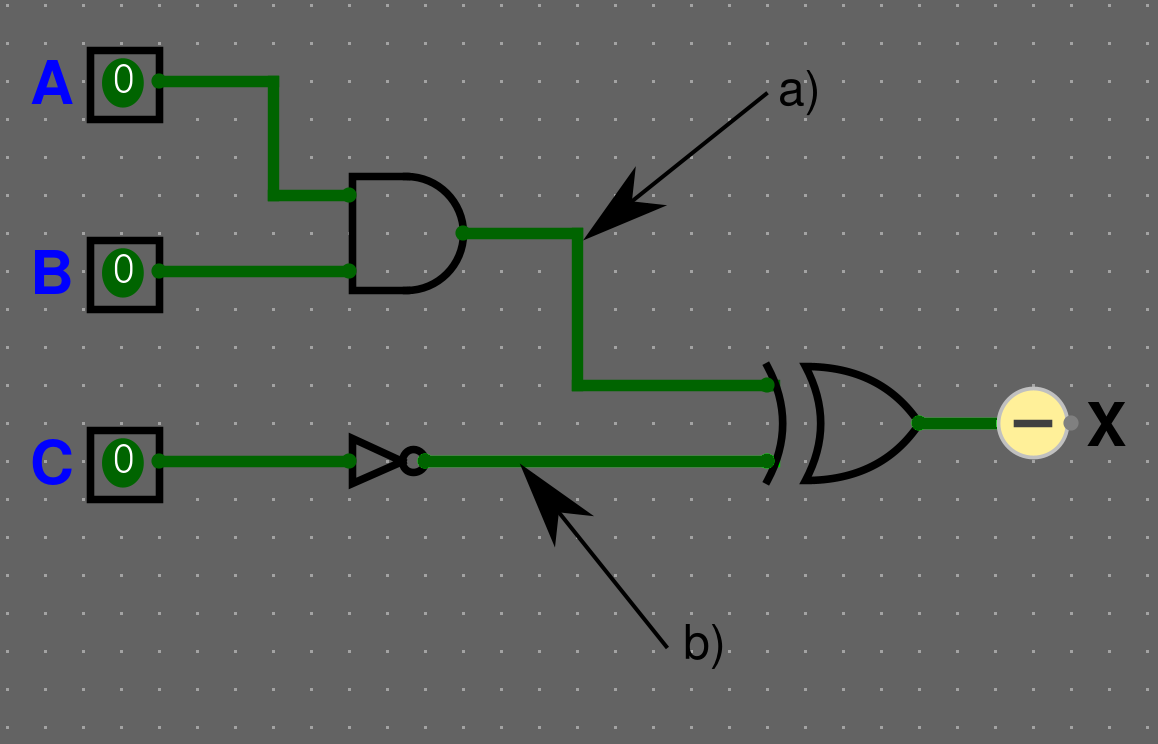
3. Zapiš výraz pro výstupy zapojení a pro označené vodiče:

Řešení

a) \(A \cdot B\)

b) \(\overline{C}\)

\(X = (A \cdot B) \bigoplus \overline{C}\)

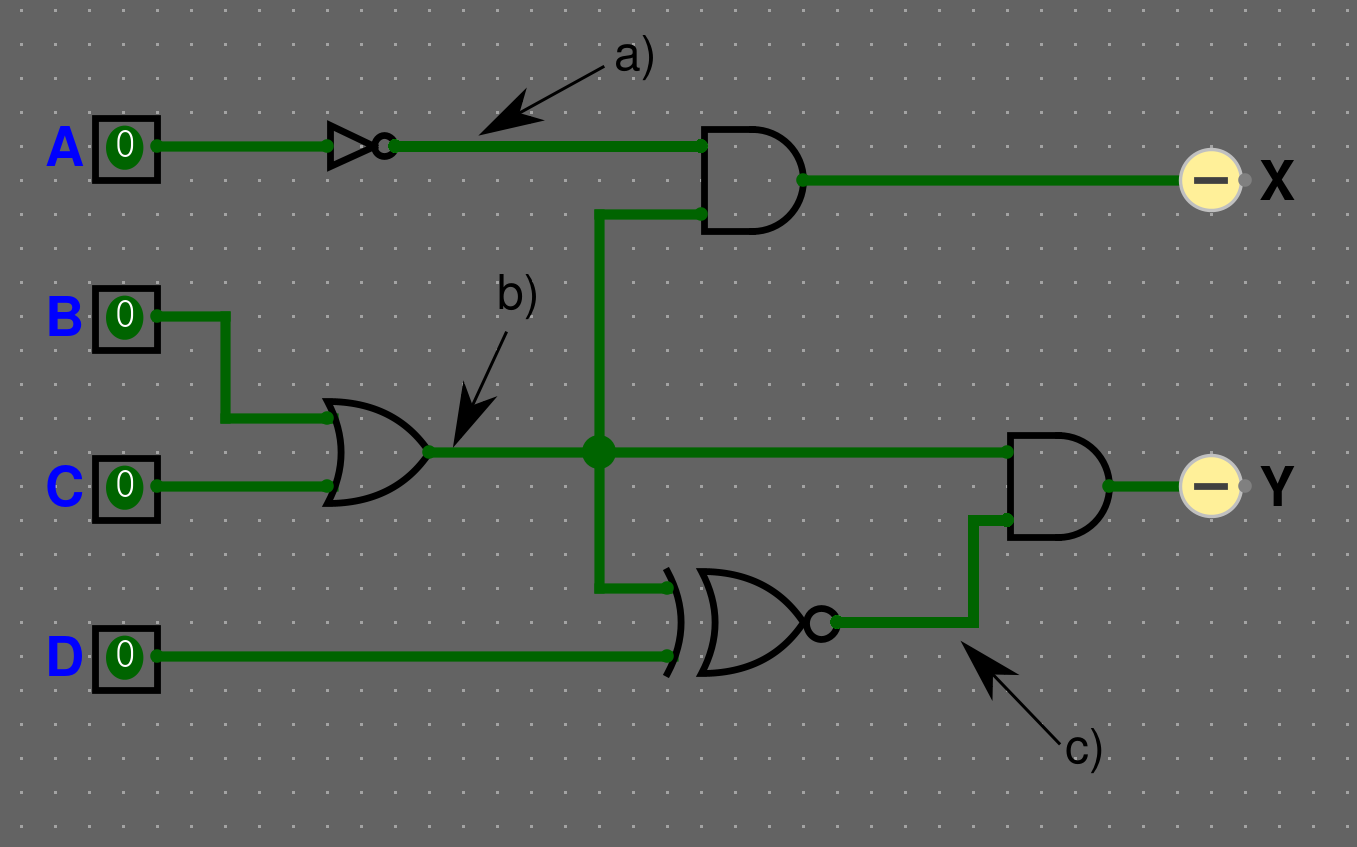
Řešení

a) \(\overline{A}\)

b) \(B+C\)

c) \(\overline{(B+C) \bigoplus D}\)

\(X = \overline{A} \cdot (B+C)\)

\(Y = (B+C) \cdot \overline{(B+C) \bigoplus D}\)

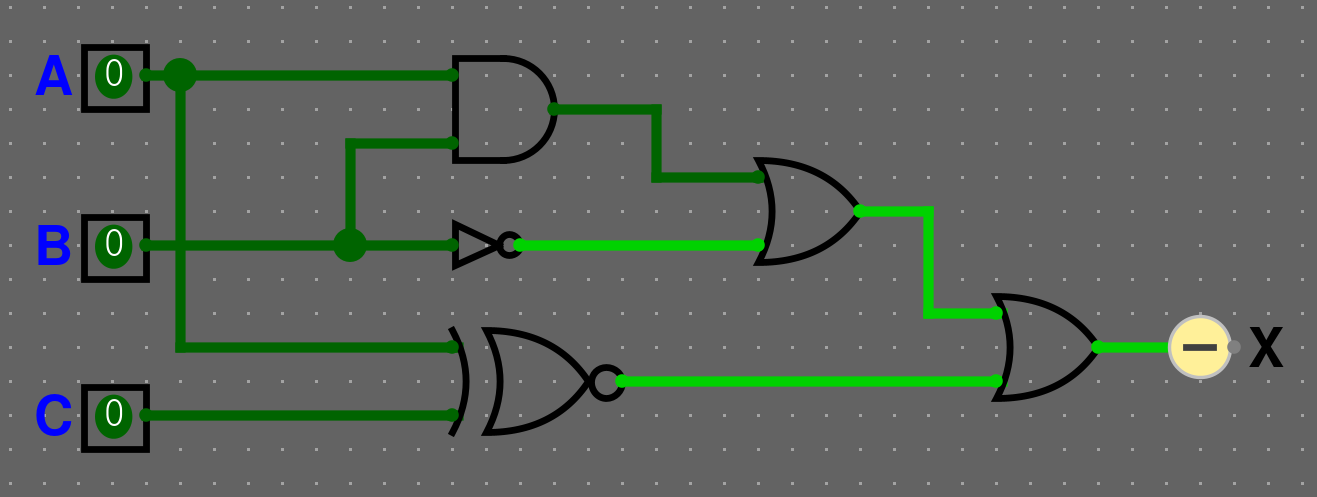
4. Nakresli zapojení pro následující výraz a nakresli pravdivostní tabulku

\(X = (A \cdot B) + (\overline{A \bigoplus C}) + \overline{B}\)

Řešení - zapojení

Řešení - tabulka

Taktéž v zapojení můžeme použít jeden OR, který příjmá 3 vstupy místo dvou (jelikož sčítání je asociativní a komutativní).

Vytváření tabulky si ulehčíme spočítáním sloupců pro námi zvolené podvýrazy (\(A \cdot B\), \(\overline{A \bigoplus C}\), \(\overline{B}\)) jejich hodnoty použijeme v dalších výpočtech, abychom se vyhnuli chybám při počítání komplikovaných výrazu z hlavy. Pokud víme na první pohled hodnoty některých řádků výsledku, můžeme je vyplnit hned do výsledku a v pomocných sloupcích je přeskočit. Nutné sloupce jsou pouze vstupy (\(A\),\(B\),\(C\)) a výstupy (\(X\)).

\(A\)	\(B\)	\(C\)	\(A \cdot B\)	\(\overline{A \bigoplus C} \)	\(\overline{B}\)	\(X\)
0	0	0	0	1	1	1
0	0	1	0	0	1	1
0	1	0	0	1	0	1
0	1	1	0	0	0	0
1	0	0	0	0	1	1
1	0	1	0	1	1	1
1	1	0	1	0	0	1
1	1	1	1	1	0	1

5. Zjednoduš následující výraz do co nejjednodušší podoby

Výsledek zde: \(\Box\)

\(X=(AC + C + B) + \overline{B \cdot \overline{C}} + \overline{C}(\overline{A}C +C)\)

Řešení

\(X = (C(A+1)+B)+\overline{B}+C+\overline{C}(C(\overline{A}+1))\)

\(X = (AC+B)+\overline{B} + C + \overline{C} \cdot (\overline{A}C)\)

\(X = AC + B + \overline{B} + C + 0\)

\(X = AC + 1 + C\)

\(X = 1\)

Výsledek zde: \(\Box + \Box\)

\(X=(A+C)(A \cdot B + \overline{\overline{A} + B}) + AC + C\)

Řešení

\(X = (A+C)(A \cdot B + A \cdot \overline{B}) + C\)

\(X = (A+C)(A \cdot (B+\overline{B})) + C\)

\(X = ((A+C) \cdot A) + C\)

\(X = A \cdot A + A \cdot C + C\)

\(X = A +C\)

Instalace Logisimu

Obecně stáhneme z oficiálního git repa v releases https://github.com/logisim-evolution/logisim-evolution/releases

Tedy

Debian based - .deb
RPM package - .rpm
Windows - .msi
macOS - .dmg
Ostatní - .jar

Arch linux

Můžeme nainstalovat z Arch AUR repozitáře pomocí yay

yay -S logisim-evolution

Template si můžete nastavit v File > Preferences... > Template > User template > Select > Vybrat template file

Logisim template

Všechny gaty jsou nastaveny na narrow

Download - template

Logisim - Základy

Po úspěšném nainstalovaní logisim-evolution (viz. návod) a spuštěním, uvidíte tohle:

Template

Jako první vám doporučuji nahrát template, kde jsou všechny gaty nastavené na narrow.

template.circ

Nahrajeme template:

File --> Open --> vybereme template.circ soubor, který jsme stáhli.

Uložíme zvlášť, abychom nepřepsali náš template:

File --> Save As --> Uložíme nový soubor (taky můžeme použít zkratku Ctrl + Shift + S)

Základy

Kurzory

Kurzory se nachází v horním menu, levým kliknutím můžeme vybrat kurzor.

Jsou celkem 4

Červený kurzor - interaktivní kurzor, měníme pomocí něj hodnoty nebo se pohybujeme v logickém obvodu
Černý kurzor - měníme zapojení, vkládáme různé komponenty
Dráty - tvoření drátů
Text - na popsání obvodu

Kurozry můžeme měnit pomocí zkratky Ctrl + [1-4]

První obvod

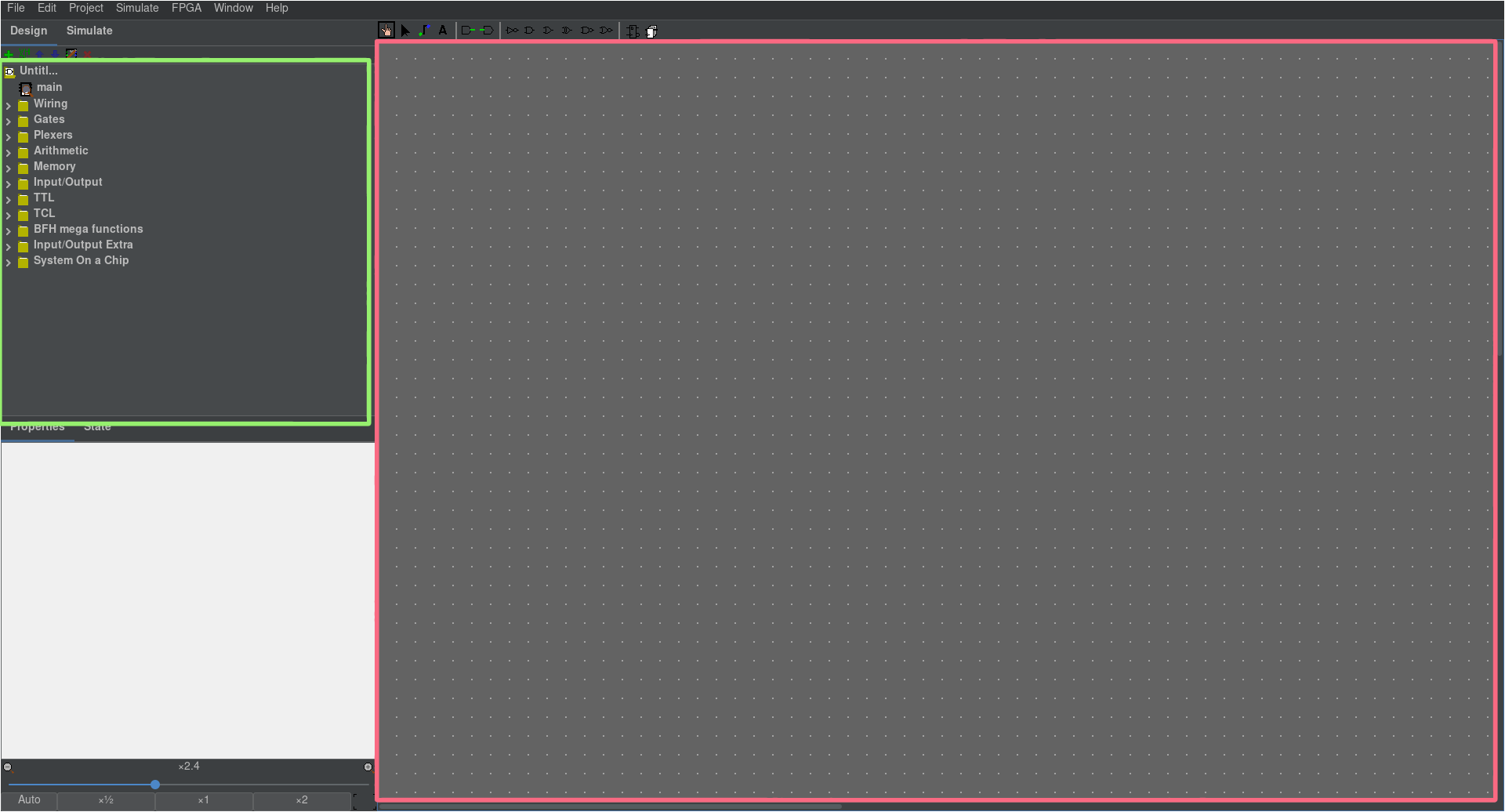
V zelénem obdelníku se vyskytují složky obsahující různé komponenty.

Zadání

Vytvořte logický obvod, který se bude chovat úplně stejně jako logický AND.

První si vytvoříme nový obvod a to tím, že klikneme pravým tlačítkem na název našeho projektu (složka ve ktéré máme obvod main). U mě je to logisim-uvod viz. obrázek

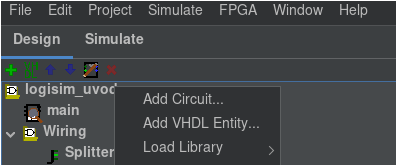
Klikneme na Add Circuit a zvolíme jméno obvodu třeba custom_and, potvrdíme a klikneme na něj dvakrát pro otevření.

První rozklikneme složku Wiring a klikneme na komponent Pin. Komponent přetáhneme do obvodu dvakrát (AND má 2 vstupy)

Poté tam dáme AND, který najdeme v Gates/AND Gate klikneme na komponentu a přidáme ji.

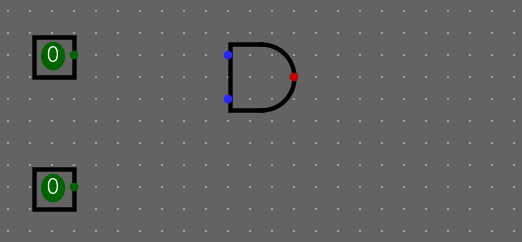
Taky musíme přidat výstup (output pin), což je vlastně Pin. Takže přetáhneme komponentu do obvodu.

Klikneme na náš pin a změníme jeho vlastnosti na následující.

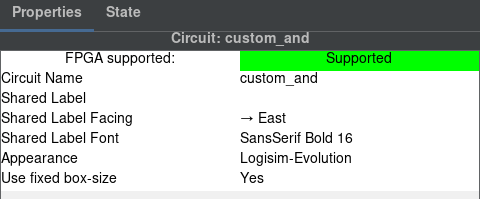
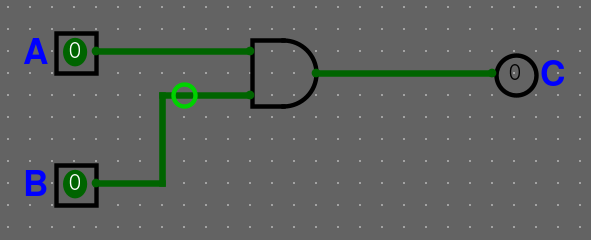
Nezbývá nám nic jiného než obvod propojit a máme následující logický obvod. Přidáme labely pro přehlednost, které taky najdeme ve vlastnostech.

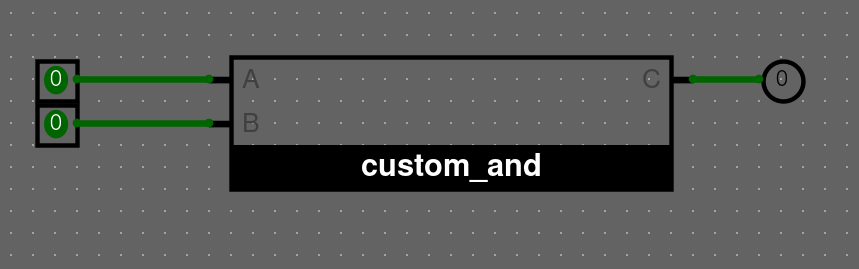
Náš nově vytvořený obvod vložíme do main

Klikneme dvakrát na main
Vybereme custom_and a vložíme do obvodu
Přidáme nějaké input a output piny pro testování

Následovně můžeme měnit hodnotu input pinů a to, že vyberem červenou ruku nahoře v nabídce nebo pomocí zkratky Ctrl + 1

Vlastnosti komponent

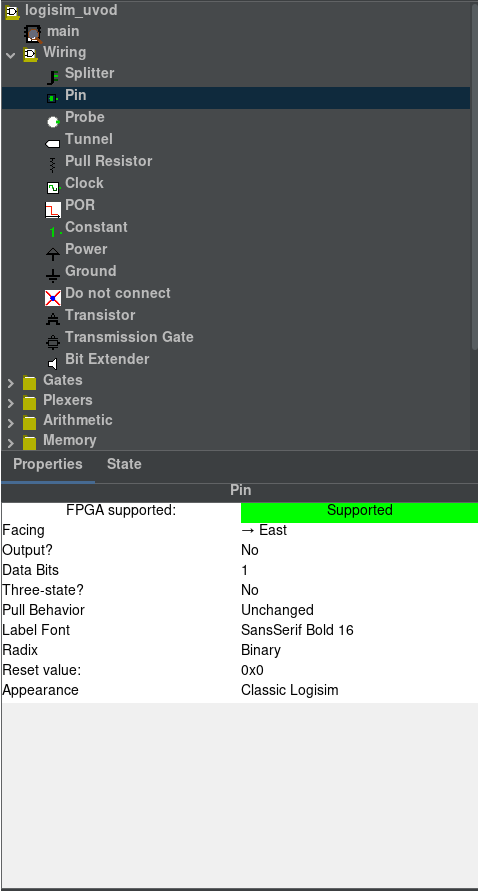
Jsou 2 možnosti jak změnit vlastnosti komponent:

Pouze pro jednu instanci komponentu
- Změníme pomocí vybrání komponentu v obvodu
Pro všechny instance kompenentu
- Změníme pomocí vybrání komponentu v nabídce

Nejčastěji upravované vlastnosti jsou:

Facing - Otočení komponenty
Label - Text u komponenty
Gate Size - Velikost hradla
Output? - Jestli je Pin output nebo ne

Cvičení

Vytvořte podobné obvody pro OR a XOR.

Třetí stav a zkraty

Váš obvod může mít 4 stavy

0 - Vypnutý stav
1 - Zapnutý stav
U - Třetí stav (undefined)
E - Zkrat

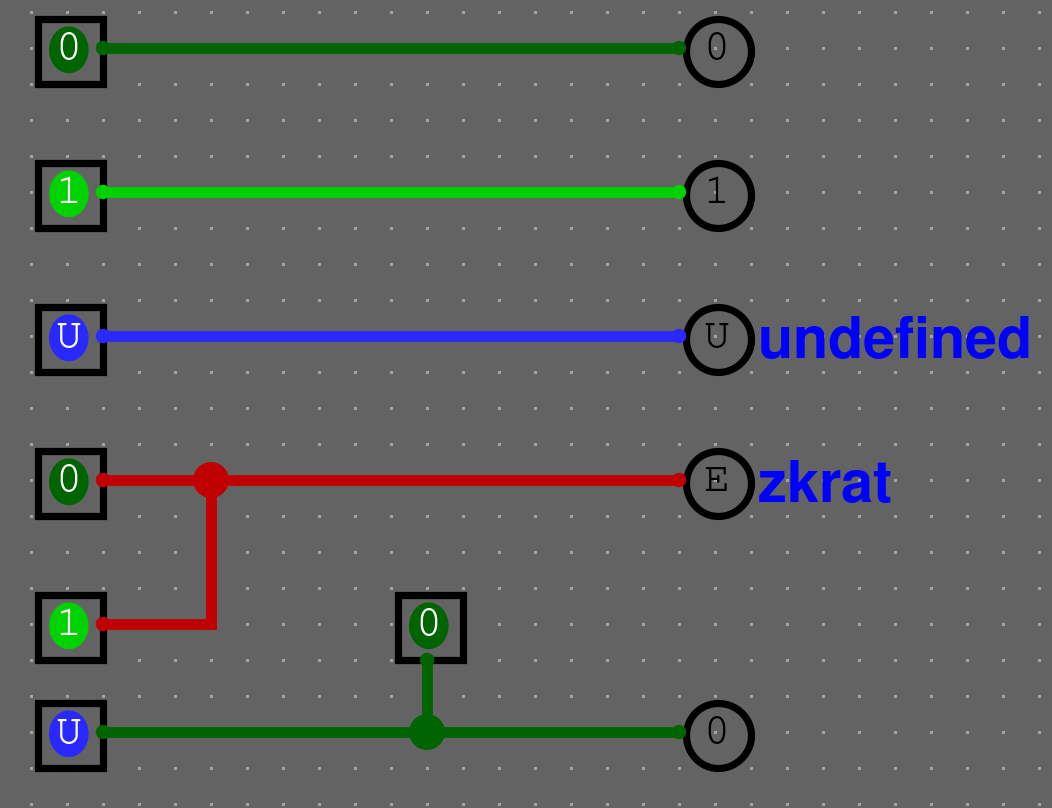
Legitimní stavy

0 - Vypnutý stav
1 - Zapnutý stav
U - Třetí stav (undefined)

Legitimní stavy jsou všechny kromě zkratu. Občas se tedy stane, že i třetí stav je žádoucí.

Třetí stav

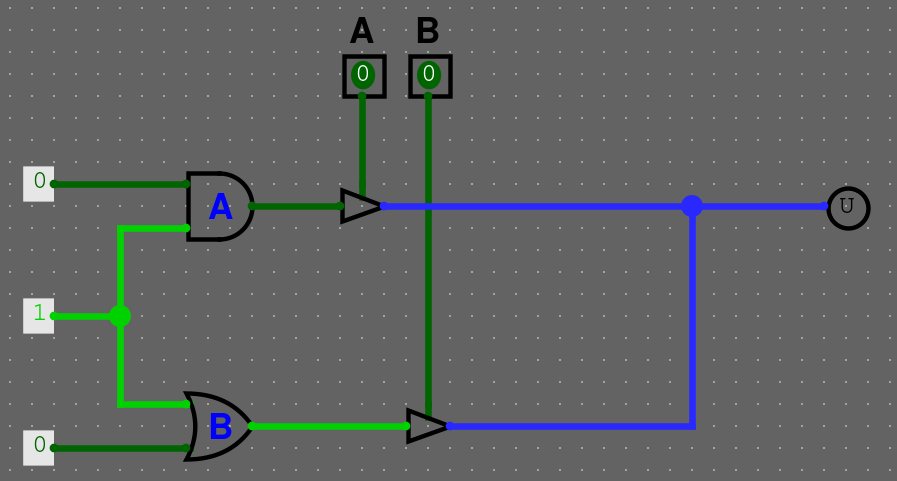
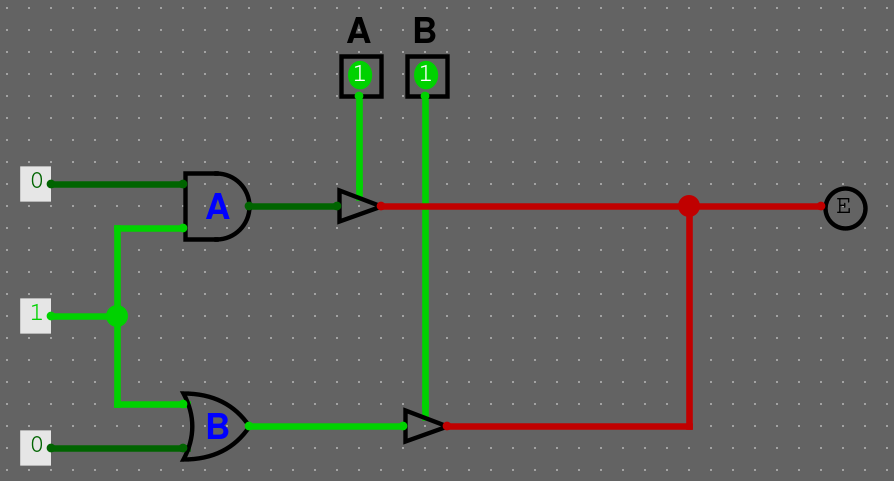
Třetí stav je nedefinovaná hodnota. Příkladné použití je pomocí Controlled Buffer (Najdeme v Gates/Controlled Buffer). Tenhle komponent vám buď propustí proud, nebo ne.

Příklad

Máme následující obvod. Pokud nic nepouštíme, máme třetí stav, hodnota není definovaná.

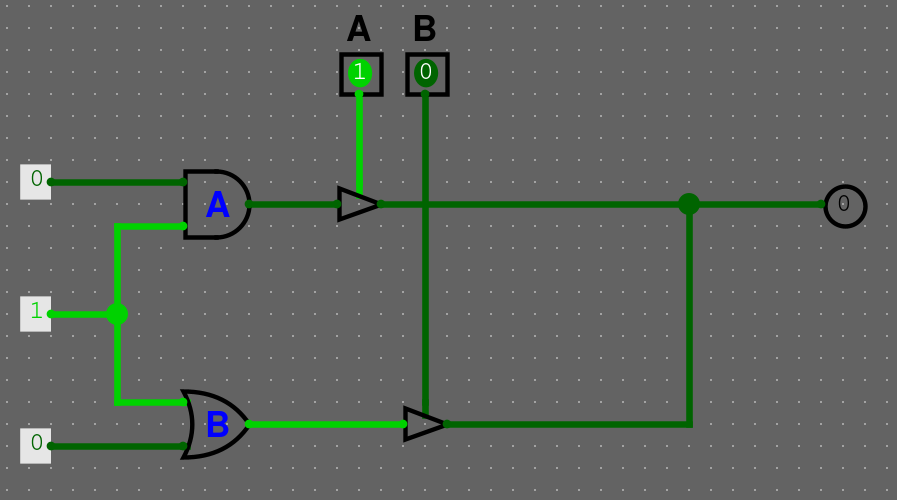
Pokud pustíme vstup A, tak dostaneme 0, pokud pustíme vstup B, tak dostaneme 1.

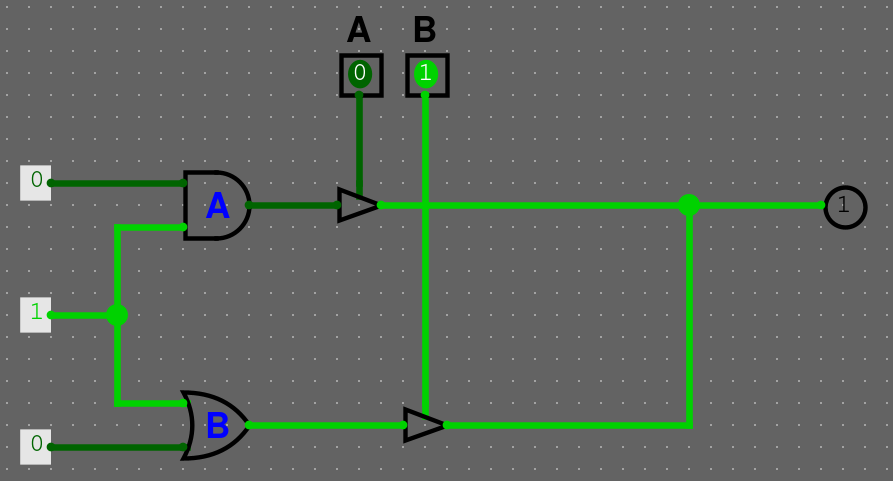
A pokud pustíme oba vstupy na jednou, dostaneme zkrat, jelikož se hodnoty liší.

Multiplexory a dekodéry

Multiplexor

Multiplexor bere \(2^n\) vstupů a \(n\) bitový selektivní vstup (SEL). Výstup má pouze jeden. Může taky obsahovat enable (ENA), který určuje, jestli je součástka zapnutá nebo ne.

Vysvětlíme si to na gifu. Na následujícím gifu jsou nějaké hodnoty A-D a pomocí 2 bitové hodnoty sel, vybíráme hodnotu, která bude na vstupu.

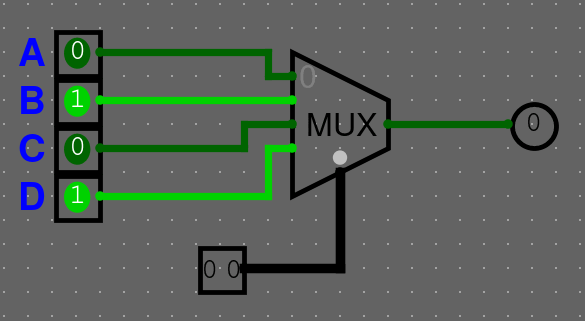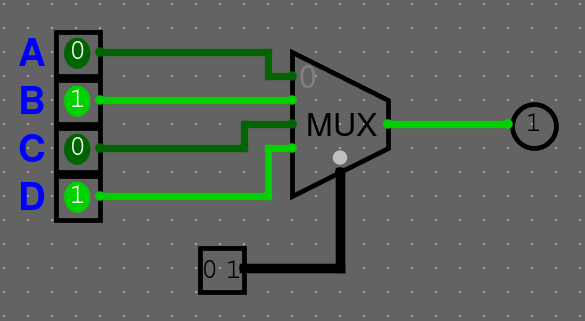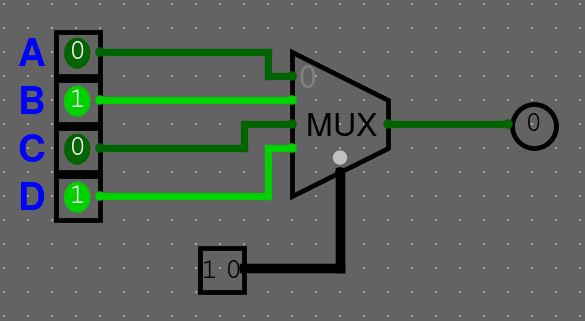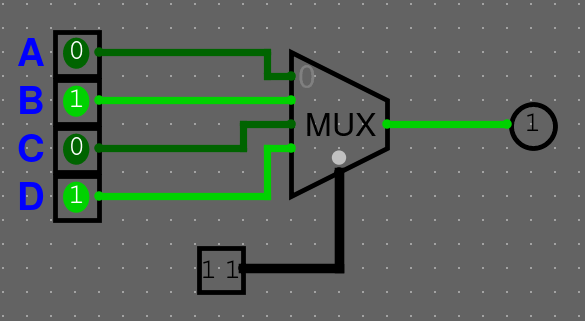
Můžeme si chování multiplexoru shrnout do tabulky

SEL	Vysílaný pin
00	A
01	B
10	C
11	D

Demultiplexor

Demultiplexor se chová obráceně z hlediska vstupů. Má jeden vstup a \(2^n\) výstupů.

Dekodér

Dekodér má \(2^n\) výstupů a \(n\) bitový vstup. Funguje podobně jako demultiplexor, ale místo našeho vstupu, tam bude vysílat vždy \(1\) viz. gif.

Cvičení

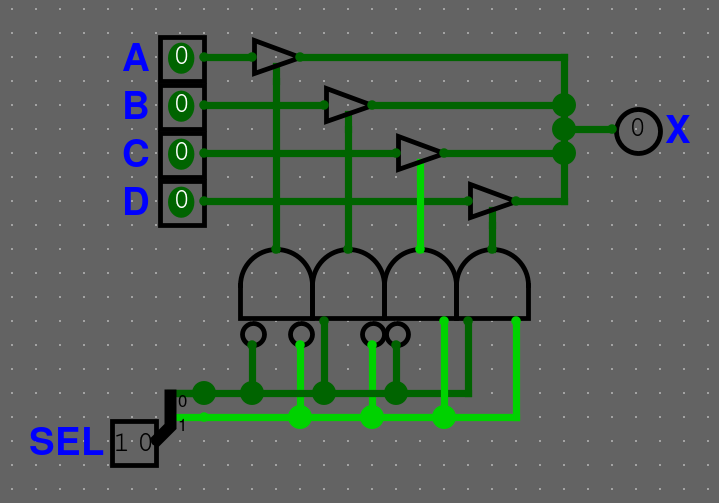
Vytvořte si vlastní multiplexor, který bude mít 2 bitový SEL vstup a 1 bitové datové bity, pomocí logických bran.

Řešení

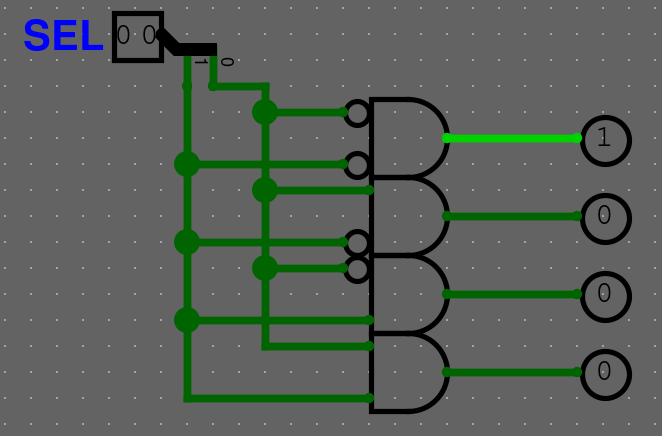
Vytvořte si vlastní dekodér, který bude mít 2 bitový SEL vstup.

Řešení

Komparátor

Cvičení

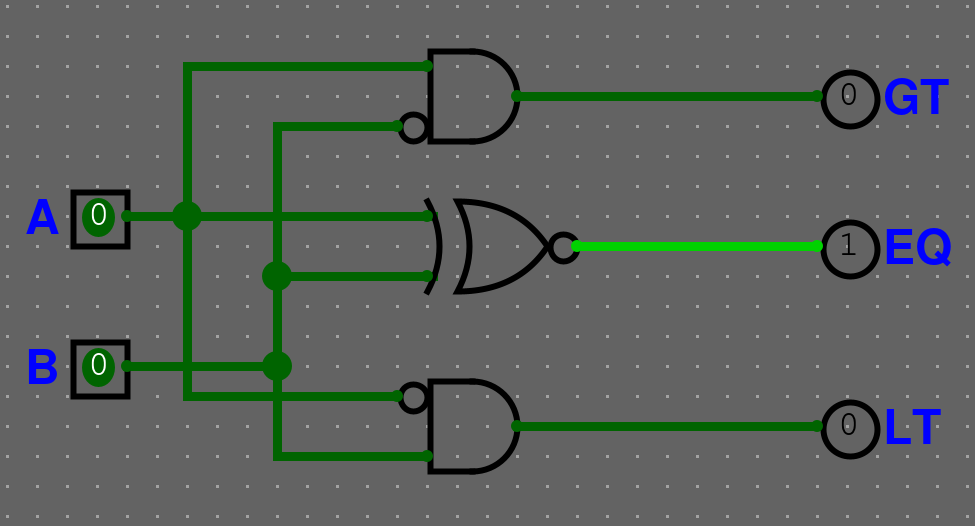
1 bitový komparátor

Postavte 1 bitový komparátor, který má 2 vstupy \(A,B\) a 3 výstupy A>B (GT), A=B (EQ), A<B (LT)

Řešení

2 bitový komparátor

Postavte 2 bitový komparátor, který má dva 2 bitové vstupy \(A,B\) a 3 výstupy A>B (GT), A=B (EQ), A<B (LT)

Řešení - Komparátor 2b

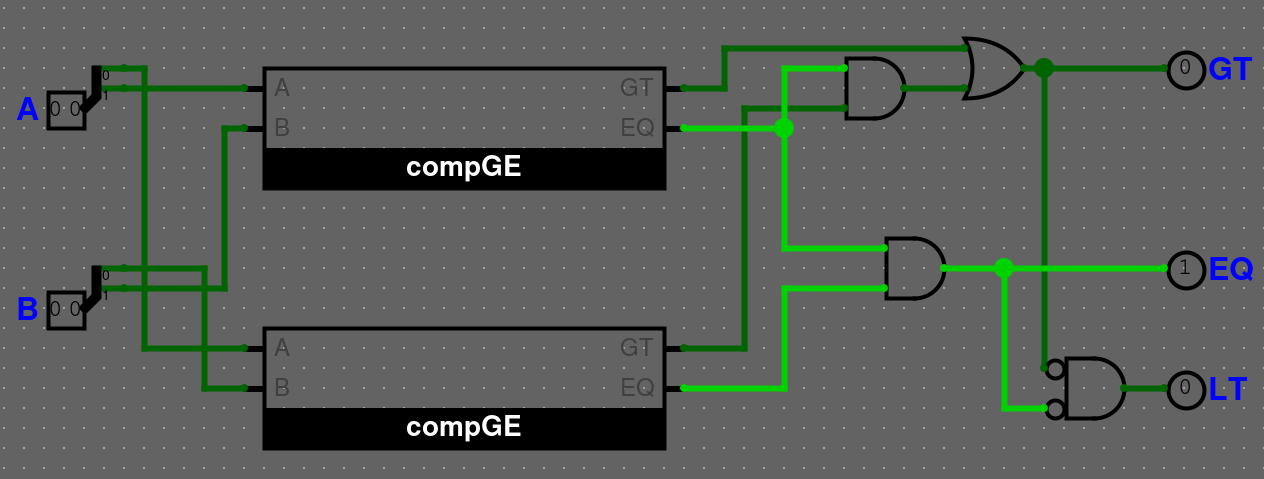
Řešení - compGE

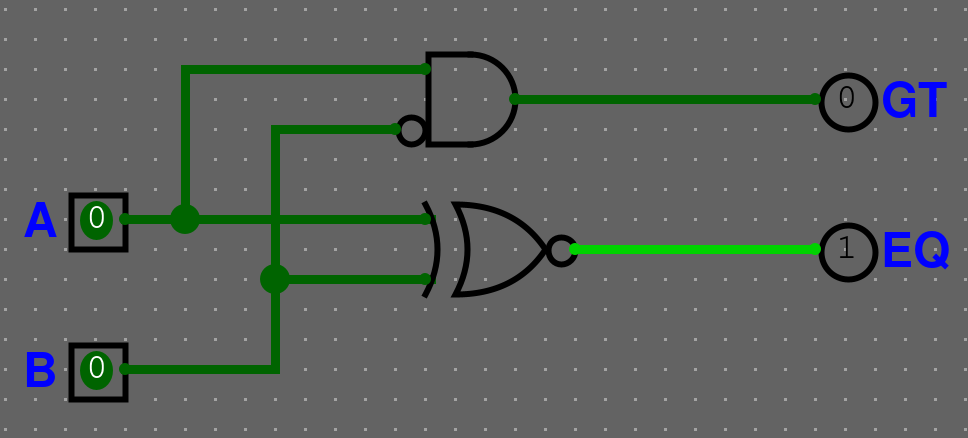
Řešení - Popis

Vytvořili jsme si compGE, abychom ušetřili dvě logic gaty, jelikož potřebujeme pro 2 bitový komparátor pouze GT a EQ.

ALU - Úvod

Každé CPU vyžaduje ALU neboli Arithmetic Logic Unit. Jedná se o "krabičku", která dokáže různé operace jako například sčítání, odčítání, bitwise operace, atd... V této kapitole se dozvíte, co je vše potřeba v ALU obsáhnout.

Vstupy ALU

vstup A a B - n-bitový vstup, záleží kolika bitové děláte ALU
CIN - Carry IN, 1 bitová dodatečná hodnota
SEL - Nebo taky Opcode, typicky 4 bitový, rozhoduje kolik vaše ALU umí operací

Výstupy ALU

OUT - n-bitový výstup, záleží kolika bitové děláte ALU
HOUT - použito pro násobení, využito pro vyšší polovinu výsledku
ZERO - 1 bitová hodnota, rozhoduje jestli jsou na výstupu samé nuly
COUT - Carry OUT z operací, 1 bitová hodnota
SIGN - Znaménko hodnoty výstupu (totožné s nejvyšším bitem hodnoty)
GT, LT, EQ - Nepovinně můžeme přidat operace z komparátoru, jde nahradit pomocí odčítání a ZERO a SIGN výstupy

UI (uživatelské rozhraní)

Pro uživatelské rozhraní můžete použít například tyhle logisim komponenty.

Komponenty vstupů

Wiring/Pin - pro 1 bitové hodnoty
Memory/Register - pro n bitové hodnoty
Input/Output/Button - tlačítko pro například operace

Komponenty výstypů

Input/Output/LED - pro 1 bitové hodnoty
Wiring/Pin - pro n bitové hodnoty
Input/Output/Hex Digit Display - pro 4 bitové hodnoty, doporučuji dost přehledné pro výstup

Příkladný main v projektu ALU může vypadat následovně.

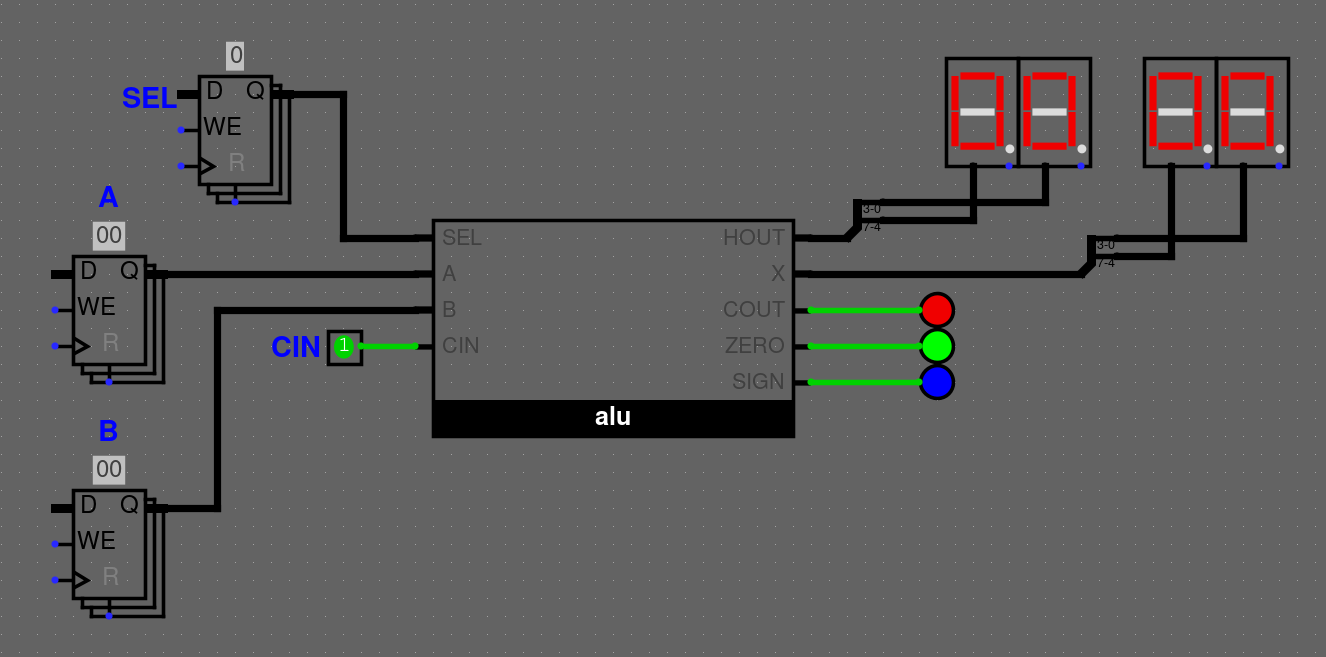
Operace ALU (`SEL`)

Bitwise operace

Jednoduché logické gaty pro n-bitové vstupy

NOT
OR
AND
XOR

Shifty

Posune nám hodnotu buď doleva SHL, nebo doprava SHR. Pokud by hodnota utekla, tedy například na hodnotu 1000 0000 budeme chtít použít operaci SHL, tak rozsvítíme COUT na 1 a OUT bude 0000 0000.

SHL - Shift left
SHR - Shift right

Příklad SHL

A	OUT	COUT
`0000 0001`	`0000 0010`	`0`
`1000 0000`	`0000 0000`	`1`
`1011 0111`	`0110 1110`	`1`
`0101 1101`	`1011 1010`	`0`

Příklad SHR

A	OUT	COUT
`0000 0001`	`0000 0000`	`1`
`1000 0000`	`0100 0000`	`0`
`1011 0111`	`0101 1011`	`1`
`0101 1101`	`0010 1110`	`1`

Rotace

Stejné jako shifty, ale při přetečení nastavíme nejmenší hodnotu na 1. Například máme hodnotu 0000 0001 a použijeme operaci ROTR, tak nastavíme OUT na 1000 0000 a označíme COUT na 1

ROTL - Rotate left
ROTR - Rotate right

Příklad ROTL

A	OUT	COUT
`0000 0001`	`0000 0010`	`0`
`1000 0000`	`0000 0001`	`1`
`1011 0111`	`0110 1111`	`1`
`0101 1101`	`1011 1010`	`0`

Příklad ROTR

A	OUT	COUT
`0000 0001`	`1000 0000`	`1`
`1000 0000`	`0100 0000`	`0`
`1011 0111`	`1101 1011`	`1`
`0101 1101`	`1010 1110`	`1`

Sčítačka

Sčítačka by měla být schopna provést více operací, jedná se o následující.

ADD - sčítání
SUB - odčítání
INC - inkrement (A + 1)
DEC - dekrement (A - 1)

Násobení

Bonusově můžete dodělat násobení neboli MUL. Zde se výsledek rozděluje na dva výstupy a to horní část HOUT a dolní část OUT.

MUL - násobení

ALU - Sčítačka/odčítačka

Sčítačka je podstatná část ALU. Po určitých úpravách z ní můžeme udělat dokonce i odčítačku. Začneme jednoduše, a to s jedno bitovou verzí.

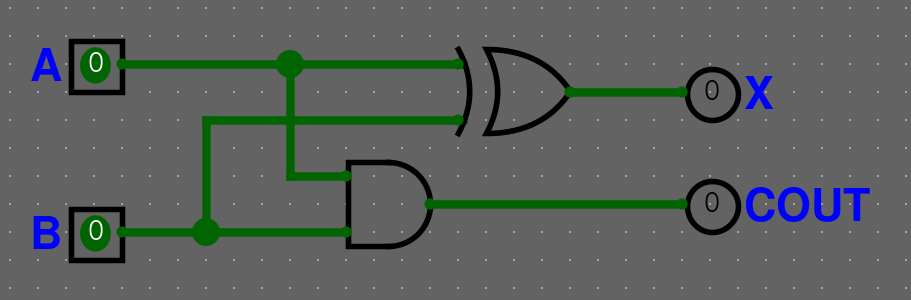
Half-adder (1 bit adder)

Pravdivostní tabulka pro half-adder vypadá následovně.

A	B	OUT	COUT
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Pomocí karnaughovy mapy nebo i logiky (odkoukání) můžeme zjistit, že sčítání (OUT) je vlastně XOR a COUT je jenom AND. Takže half-adder vypadá následovně.

Full-adder

Full-adder využívá half adder a pomocí něj přijímá další argument a to CIN, neboli carry in.

Pravdivostní tabulka pro full-adder vypadá následovně.

CIN	A	B	OUT	COUT
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Jediné, co tedy uděláme je, že přidáme half-adder 2 krát, jeden na A+B a druhý na výsledek z prvního X a CIN, neboli X+CIN.

COUT half-adderů by se měly sčítat, ale jelikož nemůže nastat případ, kdy jsou oba dva COUT 1, tak nám stačí OR. Taky se nemusíme bát přetečení, jelikož při sčítání 3 bitů se hodnota vždy vejde do 2 bitů (maximální hodnota je 3).

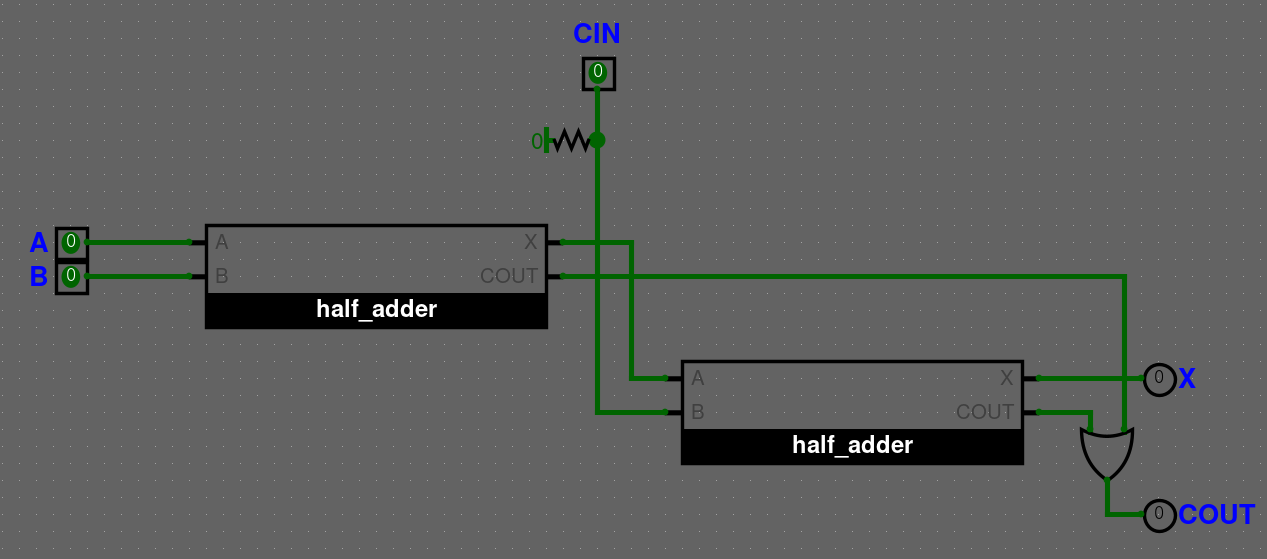
Odčítačka

Pro pochopení odčítačky si musíme říct, co jsou to záporná čísla. Záporná čísla můžeme v binárce vyjadřovat mnoho způsoby, ale nejčastější je dvojkový doplněk.

Dvojkový doplněk (two's complement)

Když pracujeme s n-bitovými čísly, tak pracujeme s tělesem \(Z_{2^n}^+\). Chceme vytvořit taková pravidla, že budeme moct pomocí sčítání odčítat.

Pro každé kladné \(b^+\) musí existovat takové \(b^-\), aby platitlo \(a-b^+ = a + (-b^+) = a + b^-\).
Taky musí platit \(b^+ + b^- = 0\)

Potřebujeme tedy najít aditivní inverzi

\(b^- = 2^n - b^+ = (2^n - 1) - b^+ + 1\)

\((2^n - 1)\) je řetězec samých jedniček a odečtením od takové hodnoty nikdy nenastane žádný přenos a odečtená hodnota se touto operací jednoduše zneguje. Dostáváme tedy pravidlo pro výpočet opačného čísla a to: \(b^- = \overline{b^+} + 1\)

Rozdělíme tak těleso na dvě poloviny na zápornou a nezápornou. Viz. obrázek

Zkráceně dvojkový doplněk spočívá ve vyhrazení prvního bitu pro znaménko. 1 znamená - a 0 znamená + s tím, že jsou u negativních čísel znegované bity a poté přičtena 1. Pochopíte z následného příkladu.

Dvojková soustava	Decimální soustava
`000`	`0`
`001`	`1`
`010`	`2`
`011`	`3`
`100`	`-4`
`101`	`-3`
`110`	`-2`
`111`	`-1`

Jeho hlavní výhoda spočívá v odčítání, jelikož pomocí tohoto znázornění platí následující: \(A-B = A + \overline{B} + 1\)

Tuto funkcionalitu tedy neimplementujeme nějak zvlášť, ale pomocí sčítačky, kde nastavíme CIN na 1 a znegujeme vstup B.

Paměti - Sekvenční obvody

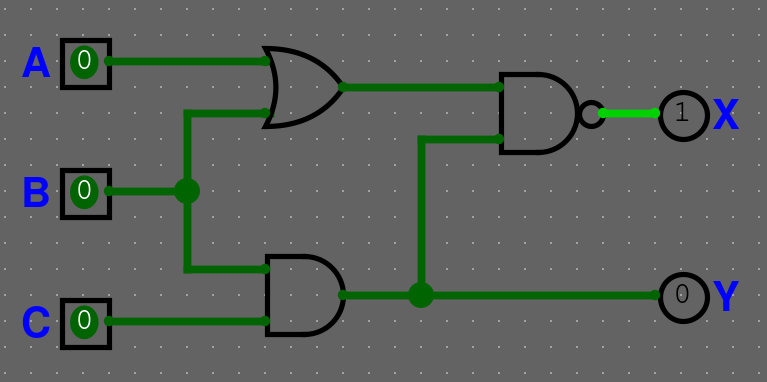
Kombinační obvody

Kombinační obvody nemají žádné smyčky. Jedná se o obvody jako například vaše sčítačka, komparátor, atd.

Příklad kombinačního obvodu

Sekvenční obvody

Sekvenční obvody narozdíl od kombinačních mají cykly. Pomocí těchto cyklů nabírají zajímavé vlastnosti a to paměti.

Příkladný sekvenční obvod s OR

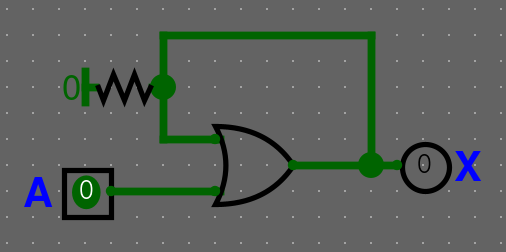
Znázornění v pravdivostní tabulce

A	X	X'
0	B	B
1	B	1
0	1	1
1	1	1

Představte si B jako jakýkoliv output buď jedna nebo 2.

0 + B - existují 2 možnosti
- 0 + 0 = 0
- 0 + 1 = 1

Vidíme, že výstup se rovná vždy B, takže do tabulky dosadíme pro B' B

1 + B - existují 2 možnosti
- 1 + 0 = 1
- 1 + 1 = 1

Vidíme, že výstup se rovná vždy 1, takže do tabulky dosadíme pro B' 1

Latch vs Flip Flop

Signály

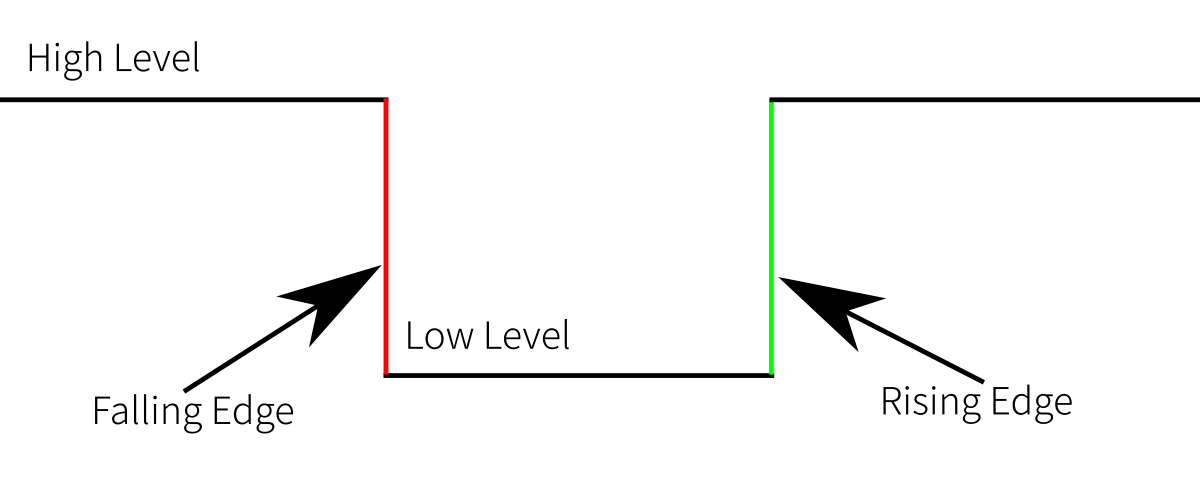
Na následujícím obrázku vidíme 4 definice.

High Level (Active-High) - zde probíhá ukládání
Low Level (Active-Low) - značí se jako CLK nebo ENA
Rising/Falling edge hodnota se zpracuje v okamžíku přechodu CLK signálu z high na low a opačně

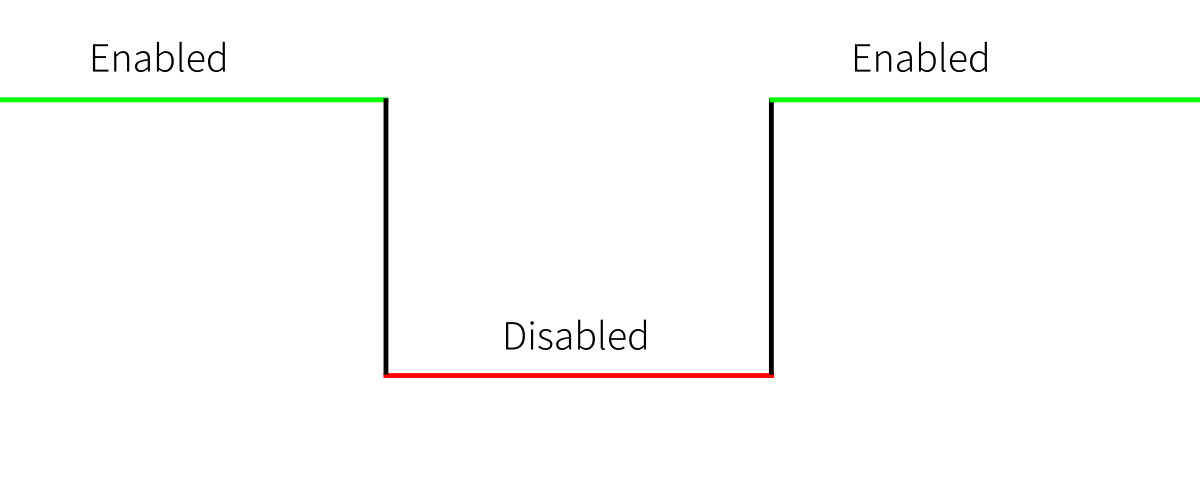
Latch

Latch je level-triggered. To znamená, že latch bere vstup, když je zapnutý viz. obrázek

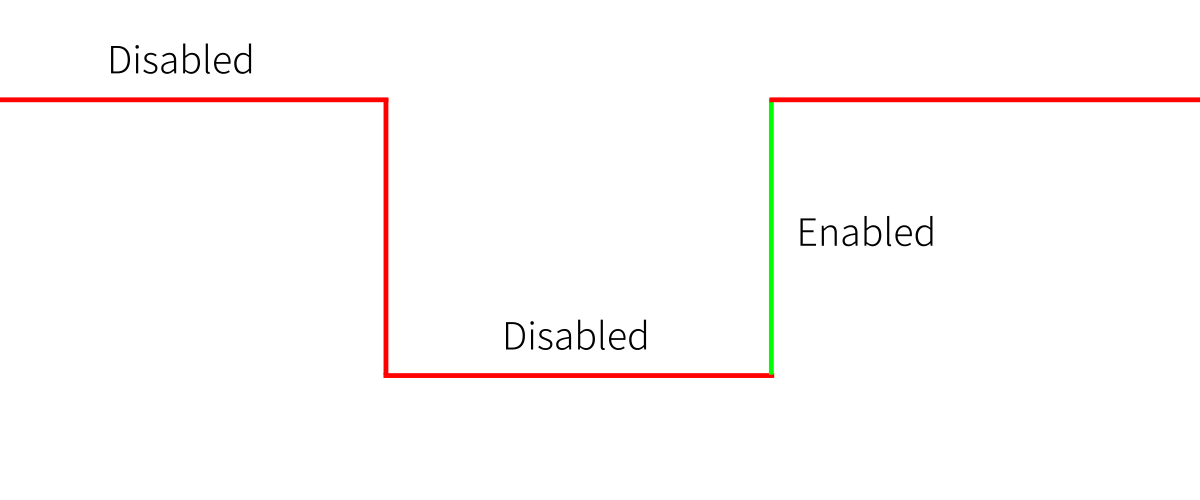
Flip Flop

Flip flop je edge-triggered. To znamená, že buď bere vstup na rising edge nebo falling edge. Na následujícím obrázku bere vstup na rising edge.

SR Latch

Sekvenční obvody můžete využít pro paměť pomocí hradla OR. Hradlo OR nám vstup zapne a nechá výstup neustále zapnutý, ale nemáme ho zatím jak vyresetovat.

Abychom ho mohli vyresetovat, přidáme další vstup a to R jako reset.

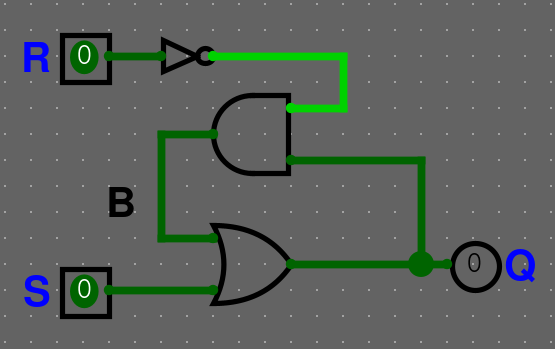
Zapíšeme do výrazu

\(Q = S + B = Q + (Q \cdot \overline{R})\)

Zapíšeme chování do pravdivostní tabulky

R	S	Q	Q'
0	0	Q	Q
0	1	X	1
1	0	X	0
1	1	X	1

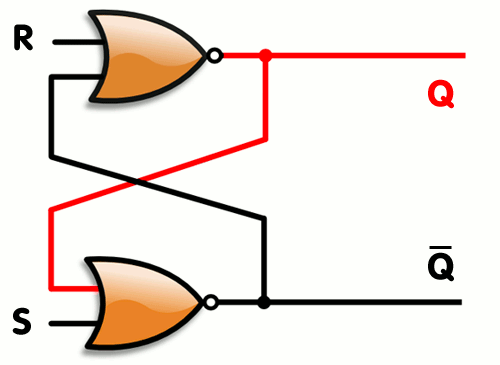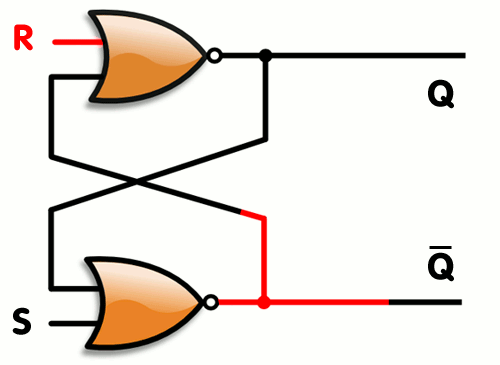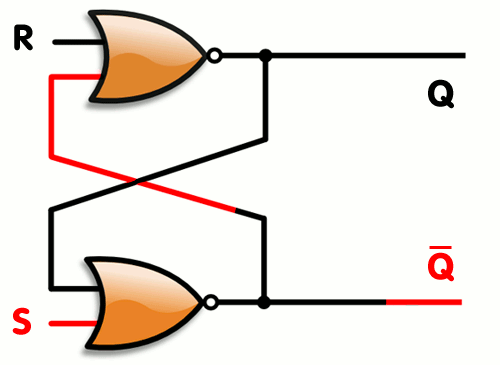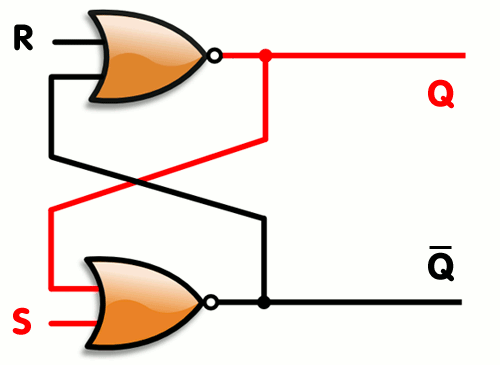
Vytvořili jsme SR Latch, který se ale dá optimalizovat, tak abychom potřebovali 2 stejné gaty a to NOR viz. gif.

Oscillation apparent

V rámci sekvenčních obvodů můžete narazit na chybu Oscillation apparent. Znamená to, že jste v nějakém paradoxním cyklu. Vyřešíte to následovně:

Odstraníme problémový prvek
Reset Simulation (CTRL+R)
Pokud není zapnuté tak --> Auto-Propagate (CTRL+E)

Bonusové materiály

Latch vs Flip Flop - https://www.youtube.com/watch?v=LTtuYeSmJ2g
Latch a Flip Flop na wikipedii
- Anglicky (víc informací) - https://en.wikipedia.org/wiki/Flip-flop_(electronics)
- Česky - https://cs.wikipedia.org/wiki/Bistabiln%C3%AD_klopn%C3%BD_obvod

Paměti - Asynchronní obvody

Asynchronní obvody fungují bez clocku, takže jakmile je na vstupu hodnota, zpracuje se.

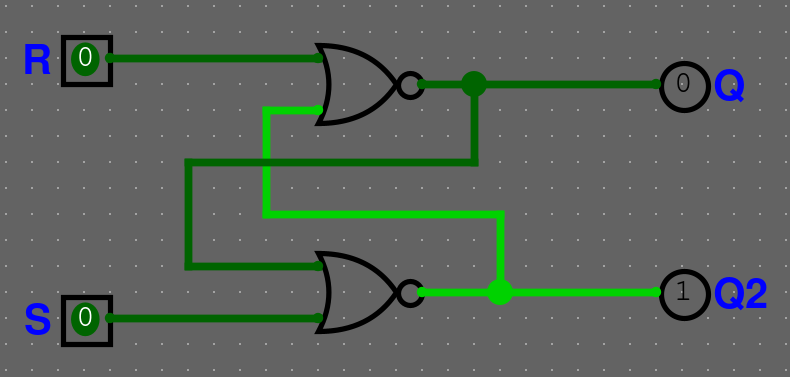
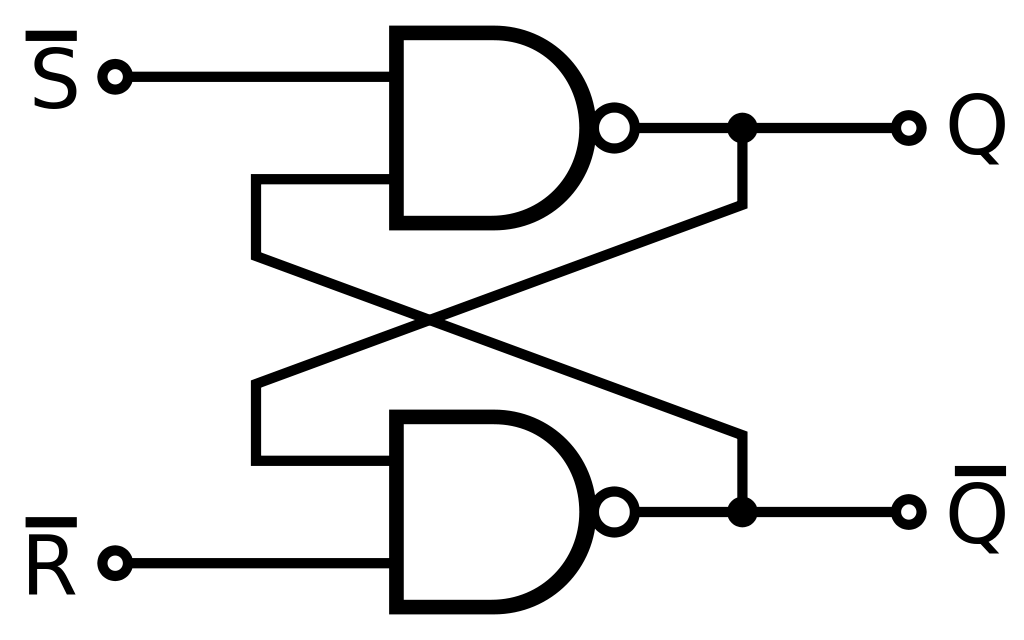
SR (Set-Reset) latch

SR latch jde vytvořit mnoho způsoby, nejčastější jsou SR NOR latch a SR NAND latch

Obrázek SR NOR latch

Obrázek SR NAND latch

JK latch

JK latch se primárně používá na toggle.

Pravdivostní tabulka JK latch

J	K	Q'	Poznámka
0	0	Q	Beze změny
0	1	0	Reset
1	0	1	Set
1	1	Q	Toggle

Gated D (Delay) latch

Gatování - možnost vypnout či zapnout prvek, pomocí vstupu (typicky ENABLE).

D latch využívá vstup enable jako 2 vstup. Tvořící sérii pravidel.

E	D	Q	\(\overline{Q}\)	Poznámka
0	X	Q'	\(\overline{Q'}\)	Beze změny
1	0	0	1	Reset
1	1	1	0	Set

Gated D latch

Paměti - Synchronní obvody

Synchronní obvody

Jsou ovládané extra clockem (CLK), který určuje kdy obvod pracuje. Příkladné obvody jsou:

SR-flip-flop
T-flip-flop
D-flip-flop

V následující kapitole se podíváme na D-flip-flop, jelikož je nejzajímavější.

Jak synchronizovat obvod? (Rising/Falling edge detektor)

Vytvoření Rising/Falling edge detektoru viz. obrázek

Rising edge detektor (pomocí NOT delaye)

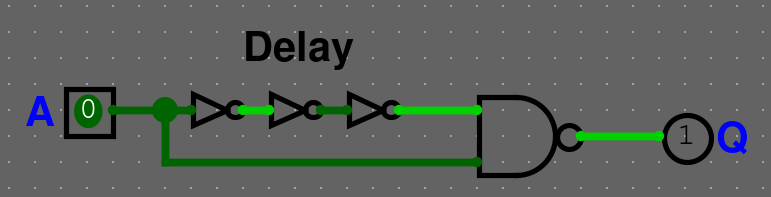
U falling edge detektoru jen prohodíme NAND gatu za AND gatu.

D (Data) Flip Flop

Pravdivostní tabulka

Clock	D	\(Q_{next}\)
`Rising edge`	0	0
`Rising edge`	1	1
`Non-rising`	X	Q

D flip-flop jde vytvořit mnoha způsoby. Ukážeme si dva, a to klasickou variantu a master-slave variantu.

Klasická varianta

Můžeme vystavět pomocí 6 NAND gate.

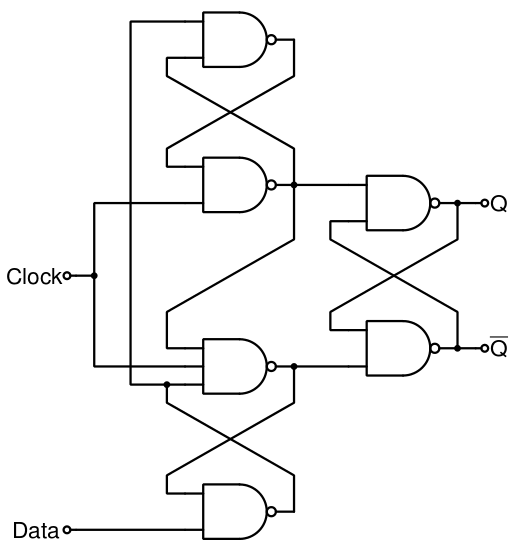
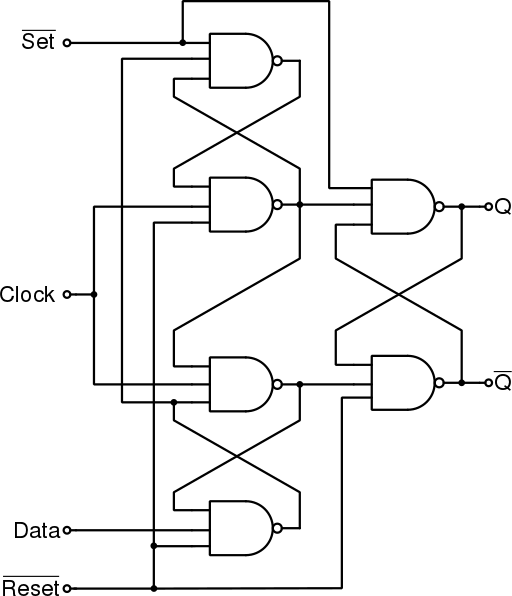
Můžeme přidat 2 vstupy a to na set a reset. Stačí nám jen NAND gaty předělat na 3 vstupové.

Master-slave-edge-triggered D-flip-flop

Vytvoříme ho pomocí 2 gated D latch. Pozor, aktivuje se na Falling edge.

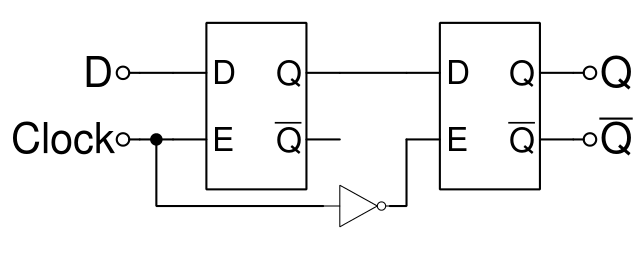
Implementace pro Rising edge

Shift Register

Shift register je jeden z nejčastějších pamětí. Je tvořen z několika D flip-flopů a můžeme do něj uložit několika bitové vstupy. Zde je příklad 4 bitového shift registru.

Při každém clocku se načte bit a uloží se do prvního flip-flopu, každý další bit se posune o jedno k výstupu, poslední bit se zahodí.

Bonusové materiály

Shift register anglická wikipedie - https://en.wikipedia.org/wiki/Shift_register
Flip-flopy a latche - https://en.wikipedia.org/wiki/Flip-flop_(electronics)

CPU - Úvod

CPU neboli Central Processing Unit je užitečný pro jakýkoliv logický problém. Zvládne využívat tupé jednotky vašeho počítače a rozhoduje, co mají dělat...

Legenda k obrázku:

červená - control flow
černá - data flow

CPU se typicky skládá z:

Control Unit (CU) - rozřazuje instrukce
Registry - často velmi rychlé paměti CPU
Kombinační logika - obecné kombinační obvody, zde patří například vaše ALU
Main Memory - typicky RAM nebo ROM
Input/Output - vstupy výstupy vašeho CPU

Sběrnice (bus)

Sběrnice typicky přenáší informace mezi komponenty ve vašem CPU. Nejlíp se to vysvětlí na datové sběrnici, která přenáší různá data mezi registry, output z ALU apod.

Typicky během instrukce pošlete nějakou hodnotu na sběrnici. Takže například chcete přesunout hodnotu registru B do registru C, tak vyšlete hodnotu registru B na sběrnici (enable) a nastavíte hodnotu registru C na hodnotu sběrnice (set).

Typy:

adresová/address - typicky pro adresy v paměti
datová/data - pro vysílaná data
řídící/control - kominukaci mezi komponenty

CPU - Návrh

Průvodce návrhem CPU.

Architektura

Harvardská - oddělená paměť programu (ROM) a paměť dat (RAM)

Von Neumannova - sjednocená paměť (RAM)

Náčrt

Doporučuji si načrtnout návrh vašeho CPU a podle toho se rozhodovat. Důležitý bod u vašeho návrhu CPU je kolika bitové jste dělali ALU. Pokud máte 8 bitové ALU, tak nemůžete mít 16 bitovou sběrnici (pokud něco nevyčarujete, možné je všechno...).

Navrhované šířky/počty

Šířka adress v ROM
Šířka hodnot v ROM
Šířka adress v RAM
Šířka hodnot v RAM
Šířka instrukcí
Počet registrů
Šířka sběrnice

I/O (Vstup/Výstup)

Alespoň jeden vstup a výstup

Příkladné vstupy

klávesnice (Input/Output/Keyboard)
registr (Memory/Register)

Příkladné výstupy

Řada ledek (Input/Output/LED)
HEX displej (Input/Output/Hex Digit Display)
TTY (Input/Output/TTY)
LED Matrix (Input/Output/LED Matrix)

Instrukce

Vaše CPU by mělo mít několik vlastností:

možnost spočítat libovolný početní problém
libovolně pracovat s registry a pamětí

Zkráceně by mělo být, co nejvíce univerzální... Tohle je dobré mít v hlavě při návrhu instrukcí.

Instrukci si můžete rozčlenit jakkoliv chcete. U mého CPU jsem měl pouze OP code a ARGy, ale můžete do instrukce schovat různé flagy apod... (technicky vzato jsou to taky argumenty, ale pouze jednobitové :D)

V excelu pak vypadají instrukce nějak takhle

Doporučené konvence

{X} - libovolný registr X
[X] - hodnota na adrese X

Doporučuji navrhnout v excelu nebo google sheets. Tabulka s jménem instrukce, krátky popis a její kód.

Typické instrukce jsou:

mov {R1} {R2} - přesune hodnotu registru z R1 do R2
movi {R1} 8b - přesune hodnotu v instrukci do R1
add {R1} {R2} - sečte R1 R2
jmp {X} - skočí na instrukci {X} v programu
...

Průběh exekuce instrukce

Fetch
- Načti hodnotu z instrukční paměti na adrese PC (Program Counter) do IR (Instruction Register)
- Přičti k PC jedna
Decode instruction
- Přečti IR, rozhodni se, zda potřebuješ další bity k instrukci
- Pokud ano, opakuj fetch, ale výsledek ulož do argument registrů,...
Execute instruction
- Podle toho, co je v IR, tak se zachovej

Vyžadované instrukce

Aritmetické

Instrukce, které se zabývají počty. Typicky vše co umí vaše ALU.

Příklady:

add A,B - přičti fixní registry A a B a výsledek ulož do A
sub {R1},{R2} - odečti libovolné dva registry a výsledek ulož do R1
shr {R1} - Proveď SHR operaci na libovolný registr R1 a výsledek ulož do R1

Paměťové

Přesuny mezi registry (kromě interních jako např. program counter)
Immediate data instrukce - instrukce, která vám dovolí nahrát libovolné číslo do registru
- movi {R1} {8b number} - nahraje do libovolného registru R1 8 bitové číslo
Práce s RAM - primárně načítání a ukládání z RAM
- load {R1} - načtení hodnoty z adresy HL (dva fixní registry pro adresu RAMky) do libovolného registru R1
- store {R1} - uložení hodnoty z libovolného registru R1 do adresy HL

Control Flow

Jumpy v programu - rozdělují se na podmíněné a nepodmíněné

Nepodmíněné:

jmp {X} - jump na určitou instrukci
jmpr {X} - jump na instrukci o X instrukcí dopředu či dozadu

Podmíněné:

jmpz {X} - skoč na X instrukci pokud je flaga ZERO rovná jedné
jumpr {X} - to stejné ale relativní jump
jmpc {X} - skoč na X instrukci pokud je flaga CARRY rovná jedné

Ostatní

Typicky I/O
led - toggle na LEDku

CPU - Stavba

Doporučuji si CPU rozdělit na 5 částí:

Registry - vnitřní paměti CPU
CU (Control Unit) - něco co vaši instrukci přijme a podle toho vykoná kroky
Control room - debug část pro čtení obsahů registrů a podobných věcí
Input/Output - vstupy,výstupy...
Paměť (RAM/ROM) - v harvardské architektuře typicky ROM pro program a RAM pro data, ve Von Neumannově architektuře pouze RAM

Hrdinské komponenty pro vaše CPU

Gates/Controlled Buffer - rozhoduje jestli pouštíte proud nebo ne, v parametrech navolíte pouze vstupní a výstupní Data Bits
Wiring/Tunnel - komponenta pro přehlednost, vytvoříte n komponent se stejným labelem (Label) a bude vám přenášet vstup bez nutných kabelů přes celou plochu
Wiring/Probe - debug věc, pro zjištění hodnoty na kabelu...
Memory/Register - nejpoužívanější paměťová buňka

Stepper

Stepper vám "stepuje" (krokuje) vaše instrukce. Jelikož některé instrukce zaberou více cyklů...

Jedná se o jednoduchý n-bitový counter s n-bitovým decoderem. Se vstupem CLK (Clock) a RST (Reset) a n-výstupy.

2 bitový stepper vypadá následovně:

Registry

Ovládání registru může vypadat následovně

Velmi doporučuji použití tunelů (Wiring/Tunnel) a vytvořit konvence jako například <registr>_set apod..

Ovládání pro register A:

a_set - 1, když setujeme register A
a_ena - 1, když pouštíme register A na sběrnici
rst - 1, když chceme provést reset registrů

Program Counter (PC)

Program counter je komponenta CPU, která vám říká, na jakém řádku programu (instrukce) se nacházíte. Potřebujete pro něj 2 věci:

zvětšit o 1
změnit hodnotu pro jmp

Na obrázku jsou piny na ovládání, to je jen pro testování.

CPU - Programování

Velmi zkrácená dokumentace pro customasm...

Pro vaše CPU budete muset vytvořit example program. Velmi doporučuji webovou aplikaci customasm

git - https://github.com/hlorenzi/customasm
web - https://hlorenzi.github.io/customasm/web/
wiki - https://github.com/hlorenzi/customasm/wiki

Jelikož má customasm svou vlastní dokumentaci, tak tuhle část projdu velmi zkráceně...

Subruledef

První si nadefinujeme podpravidla (typy) jako například registry apod.

#subruledef register
{
    A => 0x0
    B => 0x1
    C => 0x2
    D => 0x3
}

Ruledef (instrukce)

Zde nadefinujeme instrukce, viz. příkladná mv instrukce. Dejme tomu, že opcode pro mov instrukci je 1001 a šířka instrukcí je 16 bitů.

#ruledef
{
    mv {src: register},{dst: register} => 0b1001 @ src`4 @ dst`4 @ 0x0
}

mv - název instrukce
{src: register} - název parametru a typ, zde typ definovaný v subruledef register
, - separátor
{dst: register} - druhý argument dst
=> - operátor přepiš jako
0b1001 - 0b znamená zapsáno v bitech a 1001 je opcode instrukce
@ - používá se jako separátor
src`4 - argument src zakóduj jako 4 bitový
dst`4 - stejné
0x0 - 0x hexdecimální zápis čísla 0, pro doplnění do 16 bitů (naše šířka instrukce)

Dobré podotknout, že jako typ zde používám pouze register, ale velmi často použijete i další typy a to:

uXX - unsigned hodnoty
sXX - signed hodnoty
iXX - signed nebo unsigned hodnoty

Programování

Typicky začnete program s start. Velmi doporučuji psát komentáře pomocí ;

start:
    ; přesune hodnotu z registru C do registru D
    mv C,D

Celý example vypadá takhle:

#subruledef register
{
    A => 0x0
    B => 0x1
    C => 0x2
    D => 0x3
}

#ruledef
{
    mv {src: register},{dst: register} => 0b1001 @ src`4 @ dst`4 @ 0x0
}

start:
    ; přesune hodnotu z registru C do registru D
    mv C,D

Export do logisimu

Output Format: LogiSim 8-bit nebo Output Format: LogiSim 16-bit podle šířky paměti
Assemble (Ctrl+Enter) >>
Zkopírujte výstup a uložte do .txt souboru
Klikněte na vaši Memory/ROM komponentu v logisimu
Klikněte u vlastnosti Contents na (click to edit)
Open a vyberte soubor, kde jste si uložili výstup customasm

Poděkování

Děkuji všem zmíněným za pomoc v projektu APS skripta

@mvojacek - oponent projektu
- GitHub - https://github.com/mvojacek
@aestheticdisaster - pomoc s pravopisem
- GitHub - https://github.com/aestheticdisaster

Zdroje

Čitelný formát

Wikipedia

Obrázky

Gify

https://en.wikipedia.org/wiki/Karnaugh_map#/media/File:Torus_from_rectangle.gif

Tex

https://texample.net/tikz/examples/complement/

ČSN ISO 690

[1] RUST-LANG, nedatováno. Rust-Lang/mdbook: Create book from markdown files. like Gitbook but implemented in rust. GitHub [online] [vid. 25. únor 2024]. Získáno z: https://github.com/rust-lang/mdBook

[2] ANON., 2022a. Karnaughova Mapa. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://cs.wikipedia.org/wiki/Karnaughova_mapa

[3] ANON., 2022a. Adresní SBĚRNICE. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://cs.wikipedia.org/wiki/Adresn%C3%AD_sb%C4%9Brnice

[4] ANON., 2023. Control Bus. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://en.wikipedia.org/wiki/Control_bus

[5] ANON., nedatováno. Example: Visualisation of two’s complement for a 4-bit-value. TeXample.net [online] [vid. 25. únor 2024]. Získáno z: https://texample.net/tikz/examples/complement/

[6] ANON., 2024. Karnaugh map. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://en.wikipedia.org/wiki/Karnaugh_map#/media/File:Torus_from_rectangle.gif

[7] ANON., nedatováno. File:Buffer ANSI Labelled.svg. Wikimedia Commons [online] [vid. 25. únor 2024 b]. Získáno z: https://commons.wikimedia.org/wiki/File:Buffer_ANSI_Labelled.svg

[8] File:NOT ANSI labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:NOT_ANSI_Labelled.svg

[9] ANON., nedatováno. File:Buffer ANSI Labelled.svg. Wikimedia Commons [online] [vid. 28. únor 2024 b]. Získáno z: https://commons.wikimedia.org/wiki/File:Buffer_ANSI_Labelled.svg

[10] File:or ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:OR_ANSI_Labelled.svg

[11] File:NAND ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:NAND_ANSI_Labelled.svg

[12] File:nor ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:NOR_ANSI_Labelled.svg

[13] File:XOR ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:XOR_ANSI_Labelled.svg

[14] File:XNOR ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:XNOR_ANSI_Labelled.svg

[15] ANON., nedatováno. File:K-map minterms a.svg. Wikimedia Commons [online] [vid. 28. únor 2024 d]. Získáno z: https://commons.wikimedia.org/wiki/File:K-map_minterms_A.svg

[16] ANON., nedatováno. File:Sr Flip-flop diagram.svg. Wikimedia Commons [online] [vid. 28. únor 2024 e]. Získáno z: https://commons.wikimedia.org/wiki/File:SR_Flip-flop_Diagram.svg

[17] ANON., nedatováno. File:d-type transparent latch (NOR).SVG. Wikimedia Commons [online] [vid. 28. únor 2024 d]. Získáno z: https://commons.wikimedia.org/wiki/File:D-type_Transparent_Latch_(NOR).svg

[18] ANON., nedatováno. File:edge triggered D flip flop.svg. Wikimedia Commons [online] [vid. 29. únor 2024 e]. Získáno z: https://commons.wikimedia.org/wiki/File:Edge_triggered_D_flip_flop.svg

[19] ANON., nedatováno. File:edge triggered D flip flop with set and reset.svg. Wikimedia Commons [online] [vid. 29. únor 2024 e]. Získáno z: https://commons.wikimedia.org/wiki/File:Edge_triggered_D_flip_flop_with_set_and_reset.svg

[20] ANON., nedatováno. File:negative-edge triggered master slave D flip-flop.svg. Wikimedia Commons [online] [vid. 29. únor 2024 h]. Získáno z: https://commons.wikimedia.org/wiki/File:Negative-edge_triggered_master_slave_D_flip-flop.svg

[21] ANON., nedatováno. File:D-type flip-flop diagram.svg. Wikimedia Commons [online] [vid. 29. únor 2024 d]. Získáno z: https://commons.wikimedia.org/wiki/File:D-Type_Flip-flop_Diagram.svg

[22] ANON., nedatováno. File:4 bit shift register 001.SVG. Wikimedia Commons [online] [vid. 29. únor 2024 b]. Získáno z: https://commons.wikimedia.org/wiki/File:4_Bit_Shift_Register_001.svg

[23] ANON., nedatováno. File:Harvard architecture.svg. Wikimedia Commons [online] [vid. 29. únor 2024 i]. Získáno z: https://commons.wikimedia.org/wiki/File:Harvard_architecture.svg

[24] ANON., nedatováno. File:von Neumann Architecture.svg. Wikimedia Commons [online] [vid. 29. únor 2024 m]. Získáno z: https://commons.wikimedia.org/wiki/File:Von_Neumann_Architecture.svg

[25] ANON., nedatováno. File:abasiccomputer.svg. Wikimedia Commons [online] [vid. 29. únor 2024 c]. Získáno z: https://commons.wikimedia.org/wiki/File:ABasicComputer.svg