Hradla - Teorie
Obsah:
- Hradla s jedním vstupem
- Základní hradla se dvěma vstupy
- Opaky základních hradel se dvěma vstupy
- Cheat sheet
Pravdivostní tabulka
Pro značení budeme používat pravdivostní tabulku, která označuje nějaký vztah mezi vstupy a výstupy. Jedná se o jednoduchou tabulku, kde se nachází libovolně vstupů, (typicky A,B,CIN,...) a výstupů (typicky X,COUT,OUT,...). S následujících příkladů u hradel, hned pochopíte o co jde.
Hradla s jedním vstupem
Hradla, které mají jeden vstup jsou následující
- Buffer (repeater)
- NOT
Buffer (repeater)
Buffer se převážně využívá na zopakování a posílení vstupu. Taky tím "ukazujete", jakým směrem teče proud.
Symbol
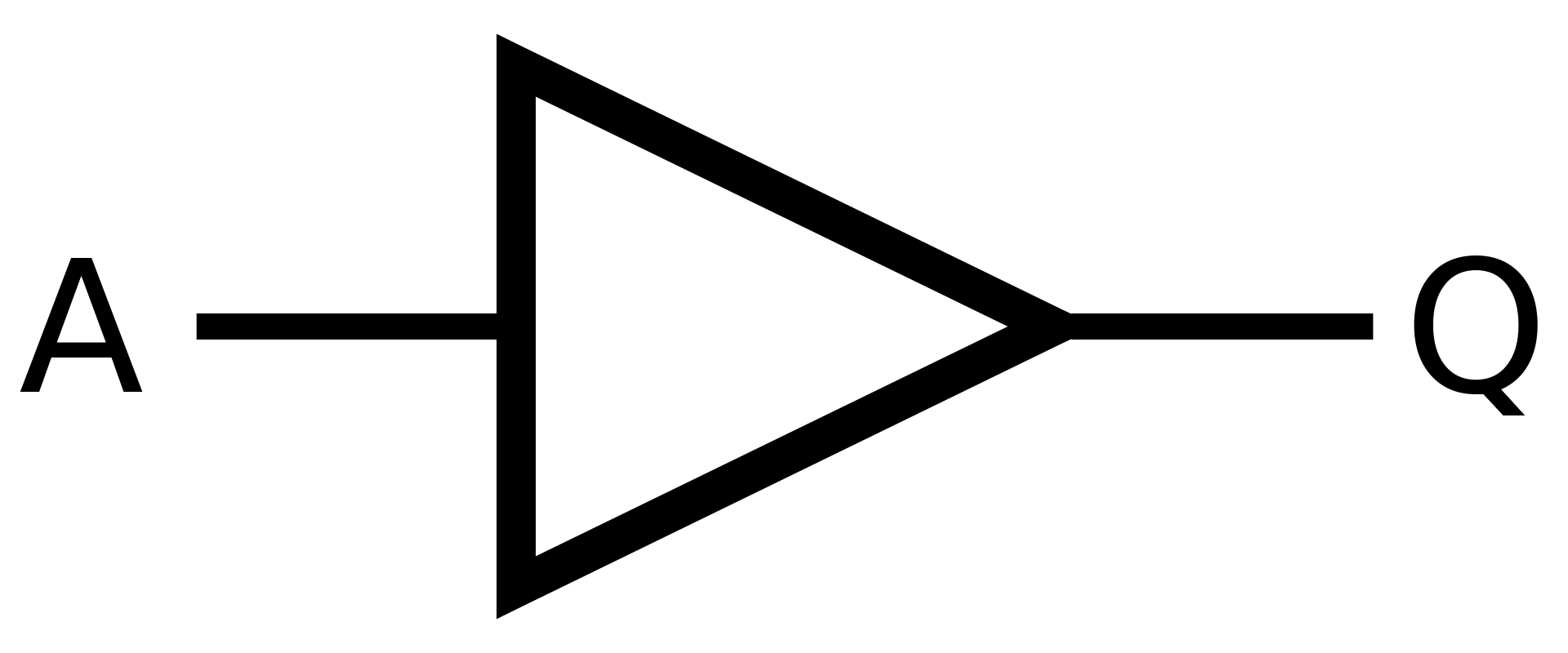
Definice
Matematická definice
\(Q = A\)
Zápis v C
bool A;
bool Q = A;
Pravdivostní tabulka
| A | Q |
|---|---|
| 0 | 0 |
| 1 | 1 |
NOT
Hradlo NOT použijete, když potřebujete změnit hodnotu na její opak.
Neboli 0 → 1 nebo 1 → 0
Symbol
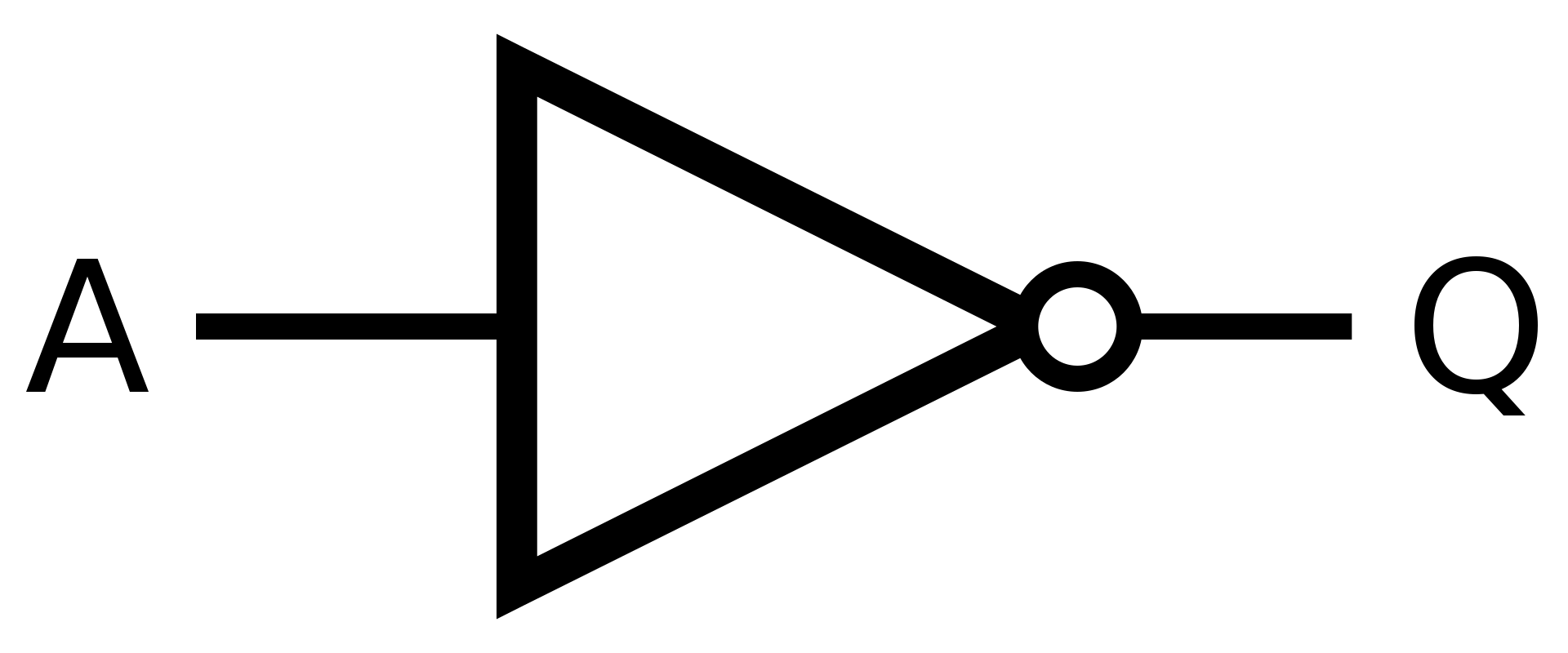
Definice
Matematická definice
\(Q = \overline{A}\)
Zápis v C
bool A;
bool Q = !A;
Pravdivostní tabulka
| A | Q |
|---|---|
| 0 | 1 |
| 1 | 0 |
Základní hradla se dvěma vstupy
Základní hradla, které mají dva vstupy jsou následující
- AND
- OR
- XOR
AND
Hradlo AND neboli logické "a" , se využívá když chcete naplnit dvě podmíky.
Pokud platí A a B, tak pošli na výstup hodnotu 1
Symbol
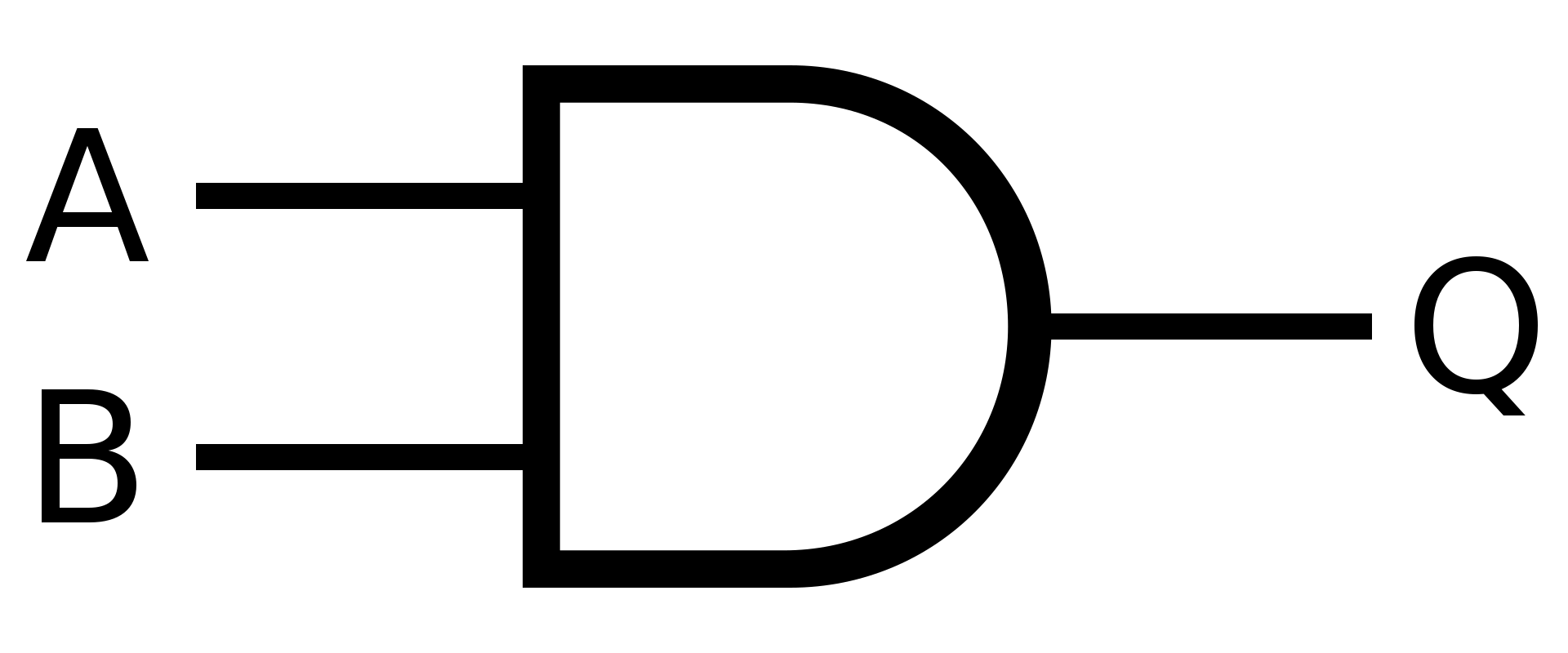
Definice
V Booleově algebře se hradlo AND rovná násobení
\(Q = A \cdot B\)
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A && B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR
Hradlo OR neboli logické "nebo" , se využívá když chcete naplnit aspoň jednu podmíku.
Pokud platí A nebo B, tak pošli na výstup hodnotu 1
Symbol
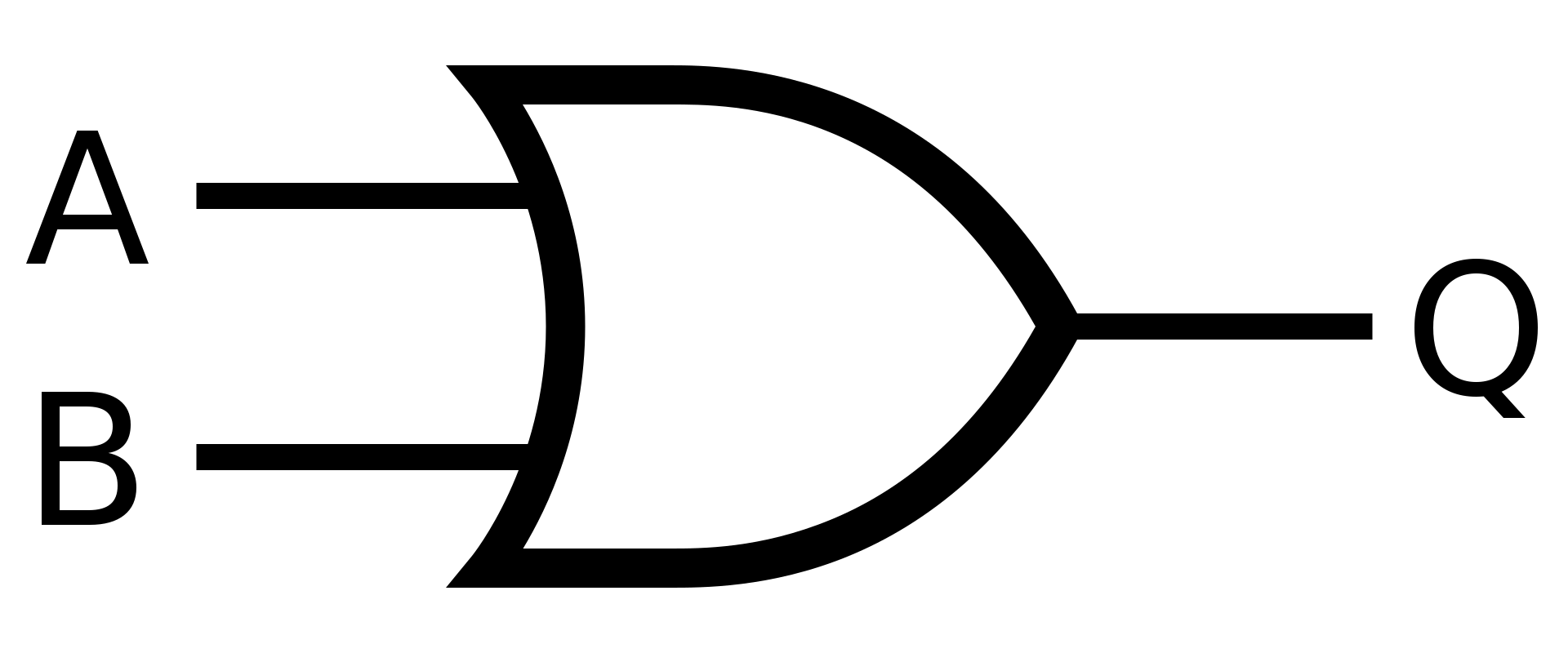
Definice
V Booleově algebře se hradlo OR rovná součtu
\(Q = A + B\)
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A || B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR
Hradlo XOR neboli exkluzivní OR , se využívá když chcete naplnit pouze jednu podmíku. Jednoduše řečeno, když se sobě nerovnají.
*Pokud platí právě A nebo právě B, tak pošli na výstup hodnotu 1 ... Pokud se A nerovná B
Symbol
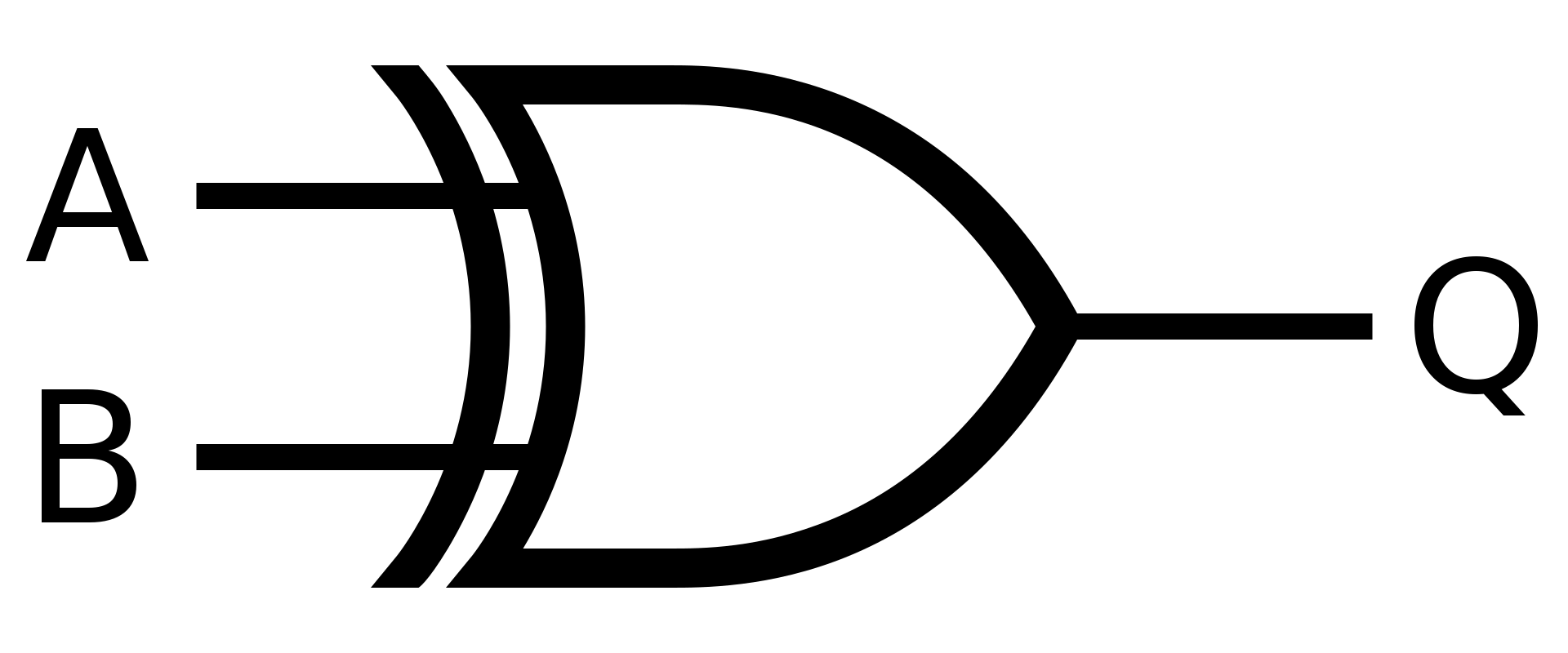
Definice
V Booleově algebře se pro hradlo XOR používá symbol \(\bigoplus\)
\(Q = A \bigoplus B\)
Zápis v C
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A ^ B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Opaky základních hradel se dvěma vstupy
Opaky základních hradel, existují právě 3
- NAND (opak AND)
- NOR (opak OR)
- XNOR (opak XOR)
NAND
Hradlo NAND má opačný výstup hradla AND
Pokud neplatí A a B, tak pošli na výstup hodnotu 1
Symbol
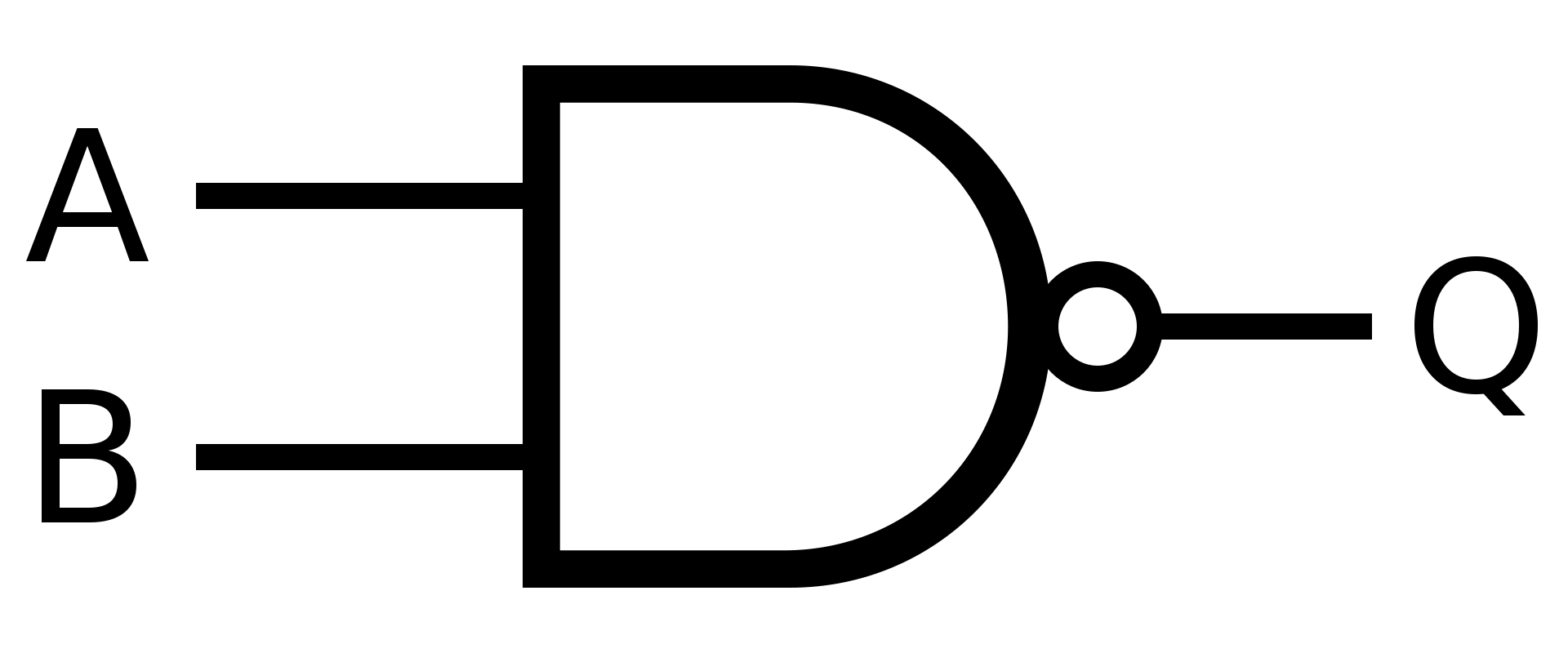
Definice
V Booleově algebře se hradlo NAND rovná negaci násobení
\(Q = \overline{(A \cdot B)}\)
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A && B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR
Hradlo NOR má opačný vstup hradla OR
Pokud neplatí A nebo B, tak pošli na výstup hodnotu 1
Symbol
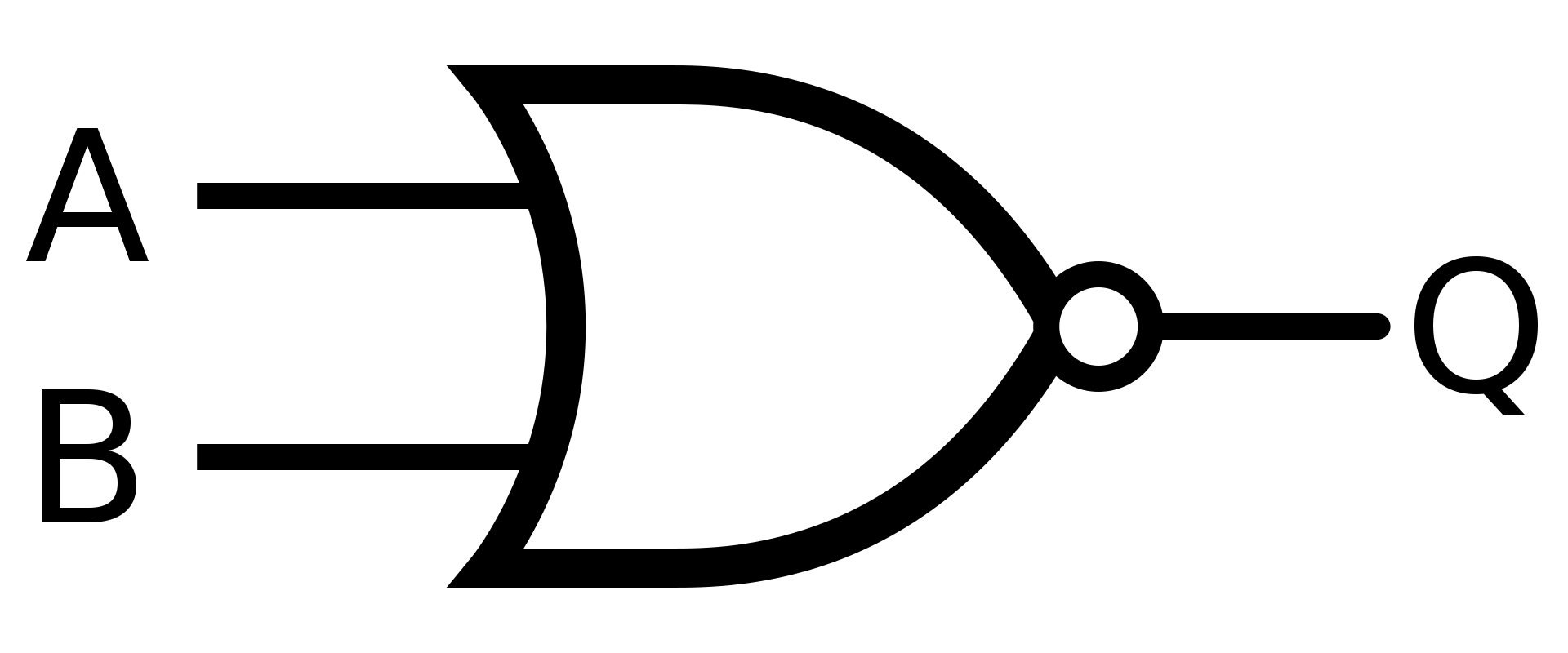
Definice
V Booleově algebře se hradlo NOR rovná negaci součtu
\(Q = \overline{(A + B)}\)
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A || B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XNOR
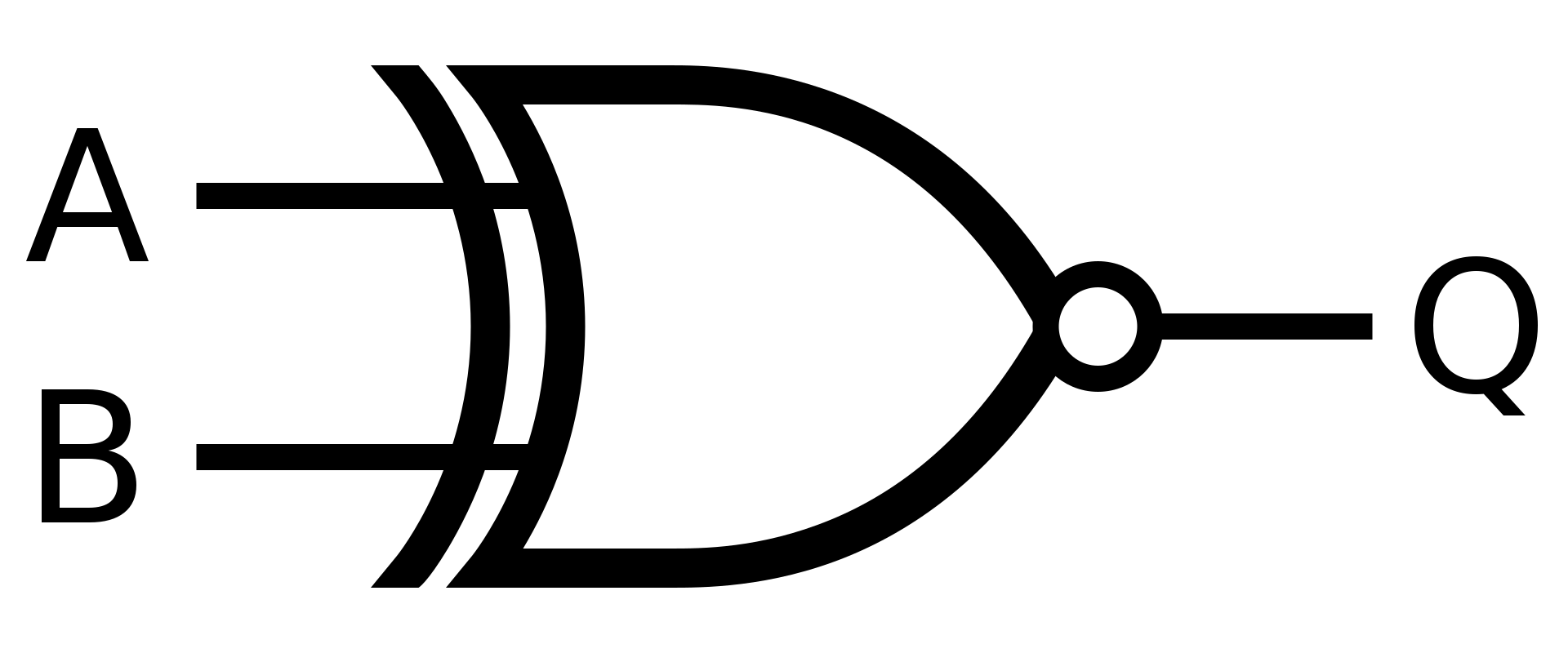
Hradlo XNOR je opak hradla XOR, jednoduše řečeno se jedná o ekvivalenci
Pokud se A rovná B
Symbol
Definice
V Booleově algebře se hradlo XNOR rovná negaci operaci ((\bigoplus))
\(Q = \overline{(A \bigoplus B)}\)
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A ^ B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Cheat sheet
Cheat sheet pro logické brány
Vstup A a Vstup B dává výstup <operace>
| A | B | AND | OR | XOR | NAND | NOR | XNOR |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
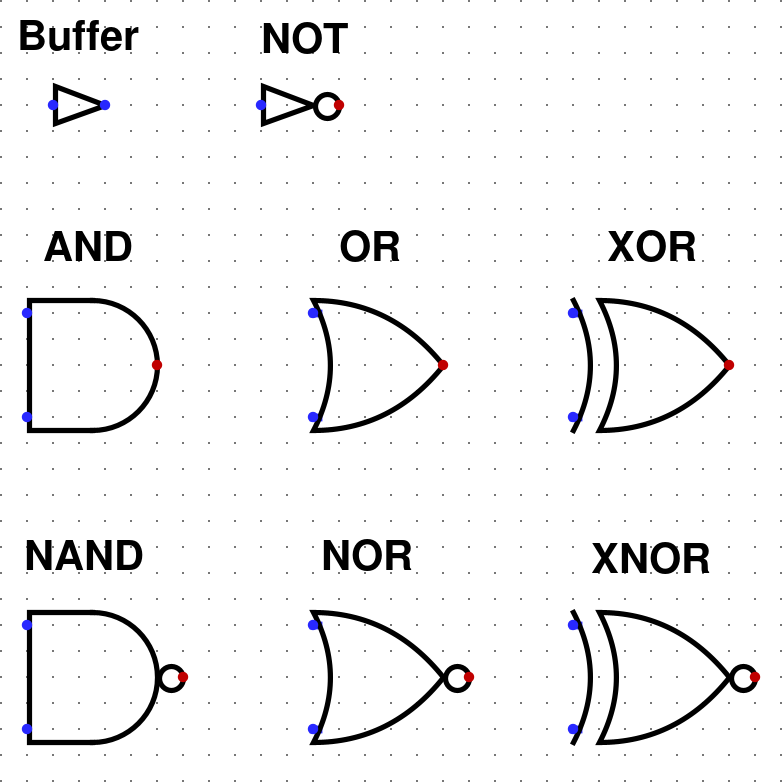
Zobrazení logických bran v logisimu