Teorie - Příprava na test
1. Nakresli logická hradla, zapiš operátor hradla jako výraz (např. X=A+B), nakresli pravdivostní tabulku:
a) NOT
Řešení - symbol
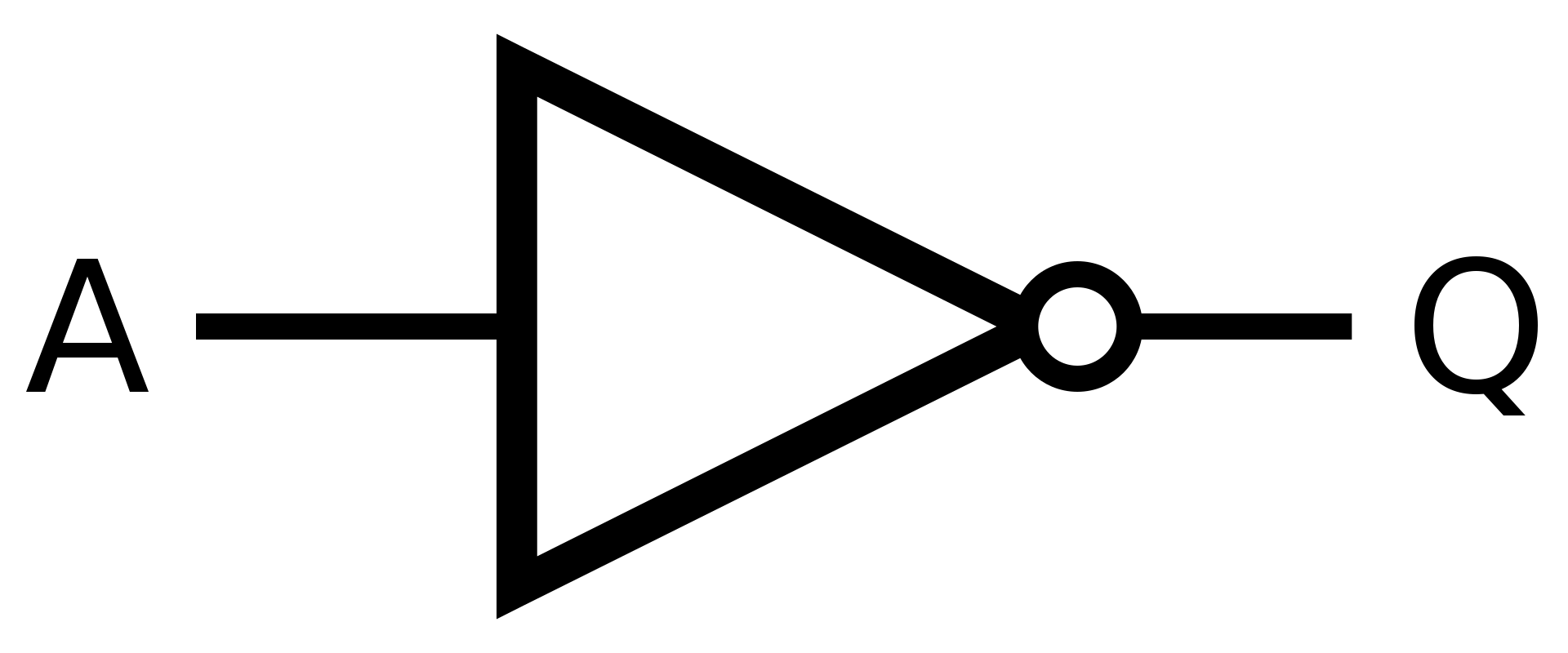
Řešení
\(X = \overline{A}\)
| A | X |
|---|---|
| 0 | 1 |
| 1 | 0 |
b) OR
Řešení - symbol
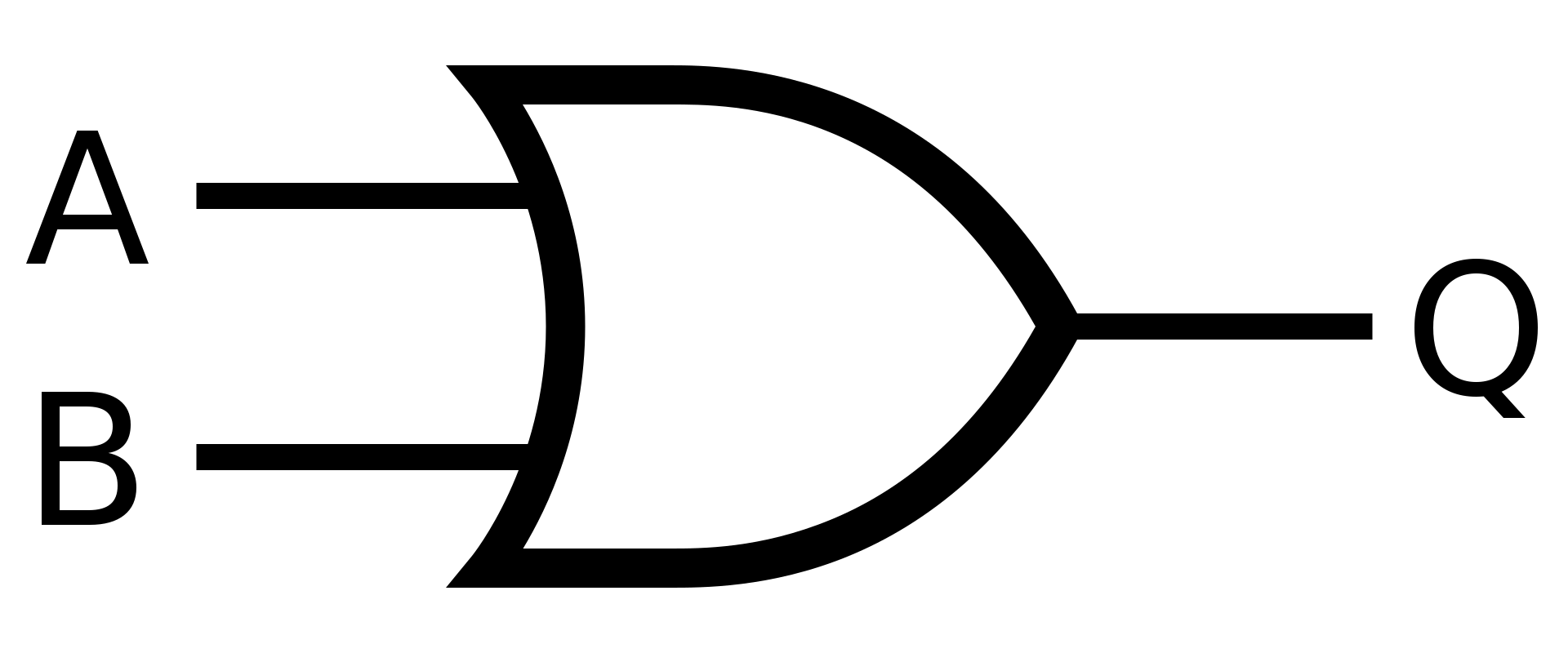
Řešení
\(X = A + B\)
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
c) XNOR
Řešení - symbol
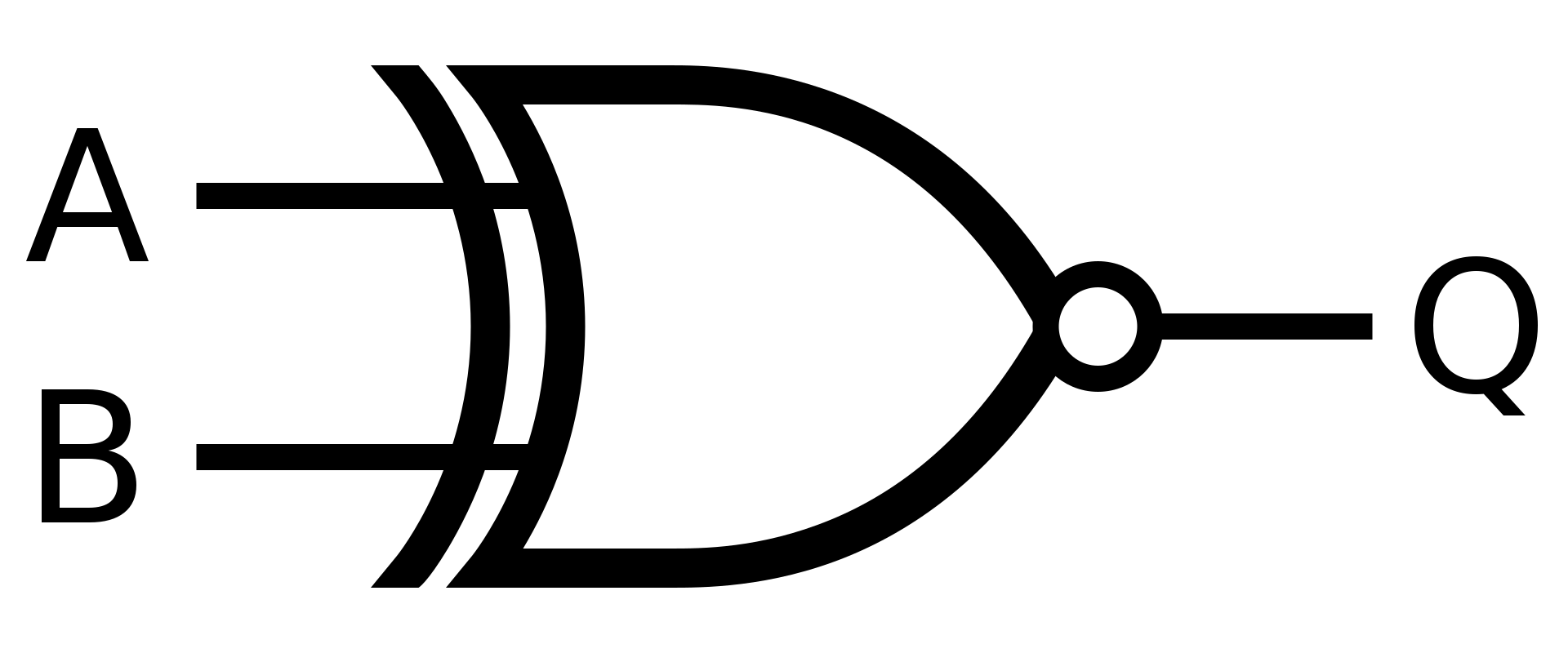
Řešení
\(X = \overline{(A \bigoplus B)}\)
| A | B | X |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
d) AND
Řešení - symbol
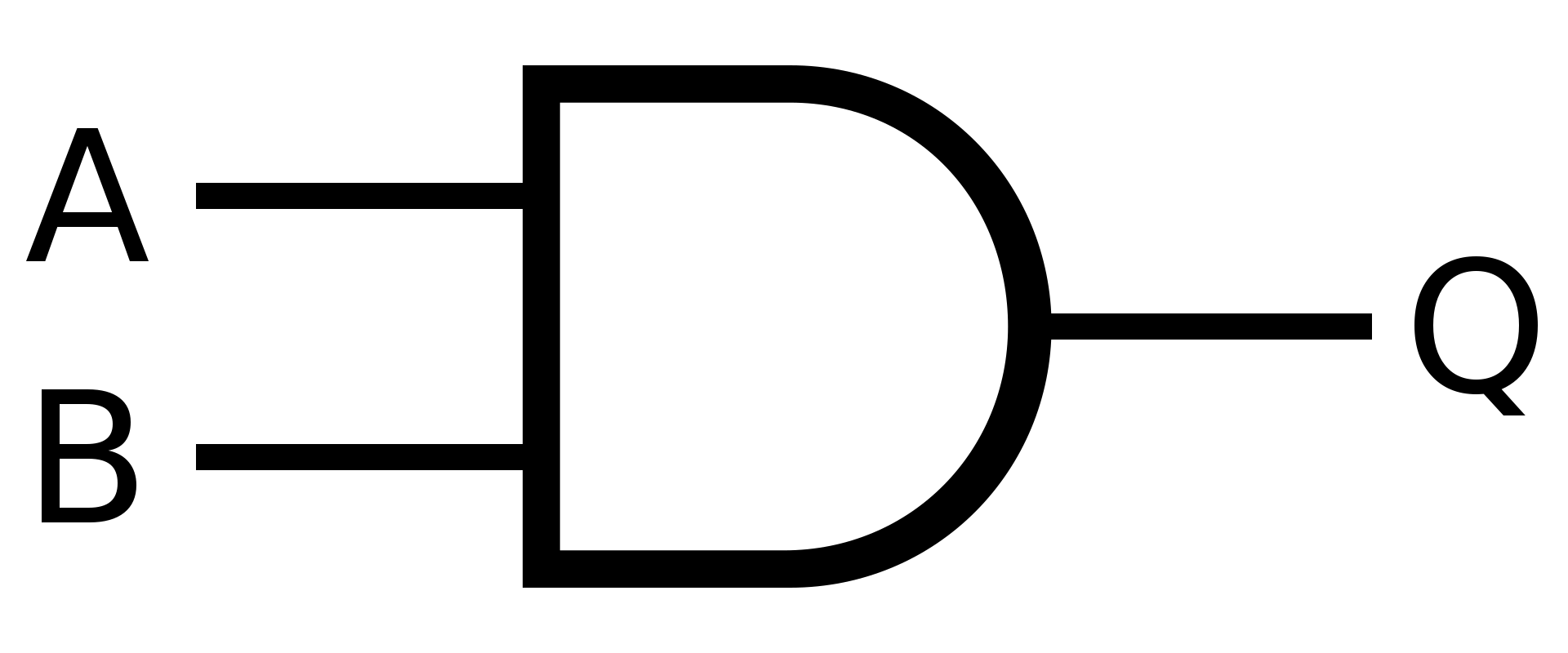
Řešení
\(X = A \cdot B\)
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. Pojmenuj následující hradla, zapiš jejich výraz a pravdivostní tabulku
a) 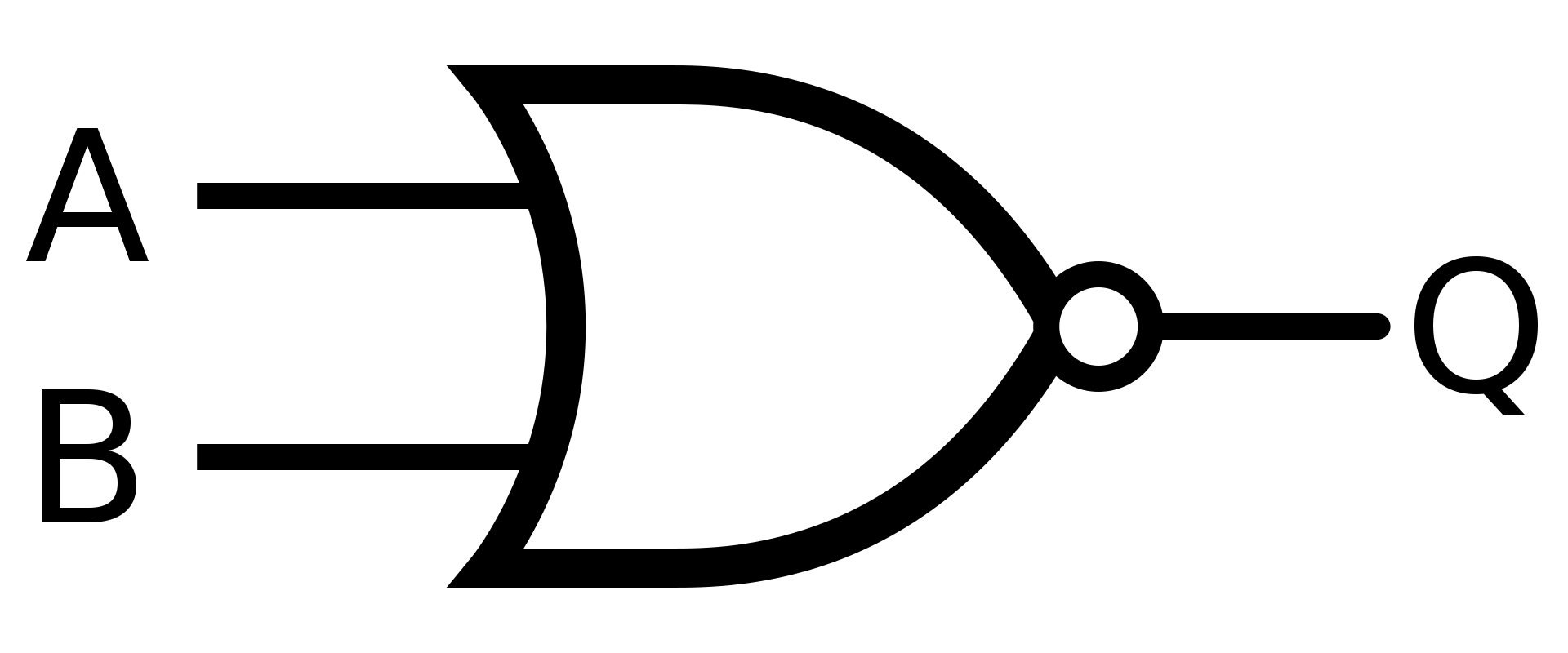
Řešení
NOR
\(X = \overline{(A + B)}\)
| A | B | X |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
b) 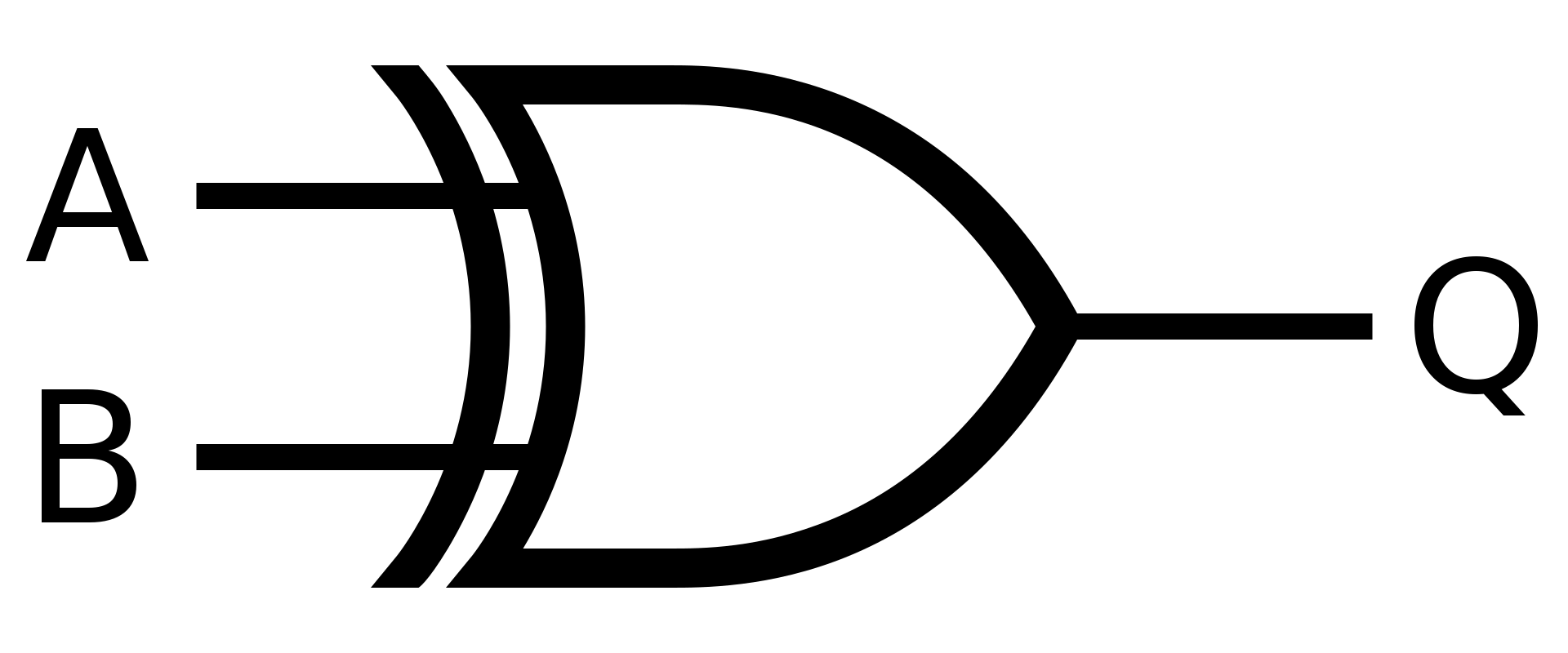
Řešení
XOR
\(X = A \bigoplus B\)
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
c) 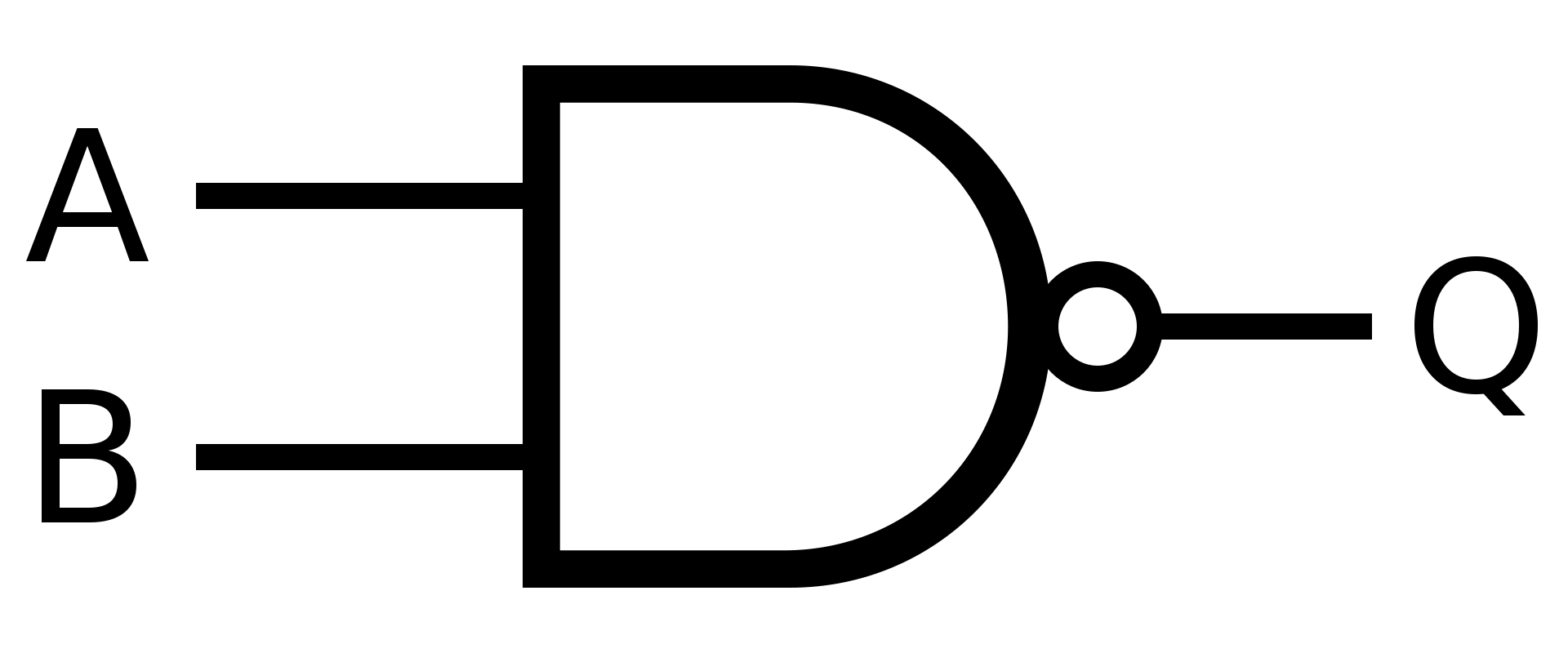
Řešení
NAND
\(X = \overline{(A \cdot B)}\)
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
3. Zapiš výraz pro výstupy zapojení a pro označené vodiče:
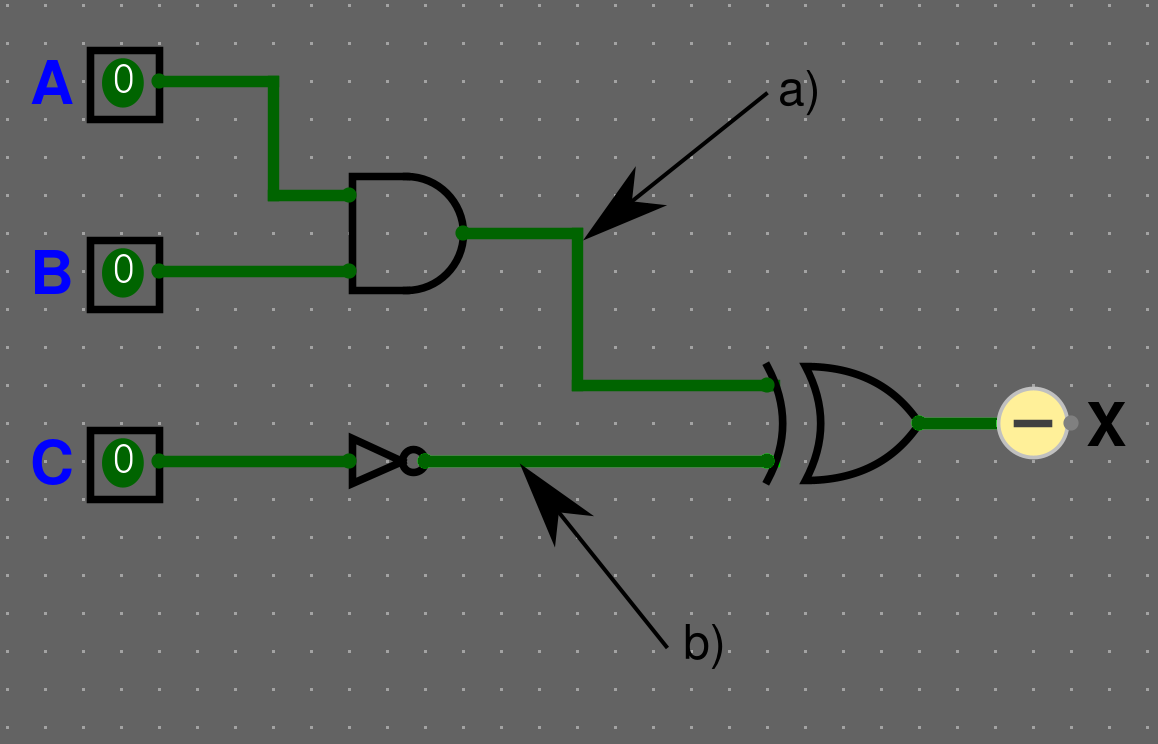
Řešení
a) \(A \cdot B\)
b) \(\overline{C}\)
\(X = (A \cdot B) \bigoplus \overline{C}\)
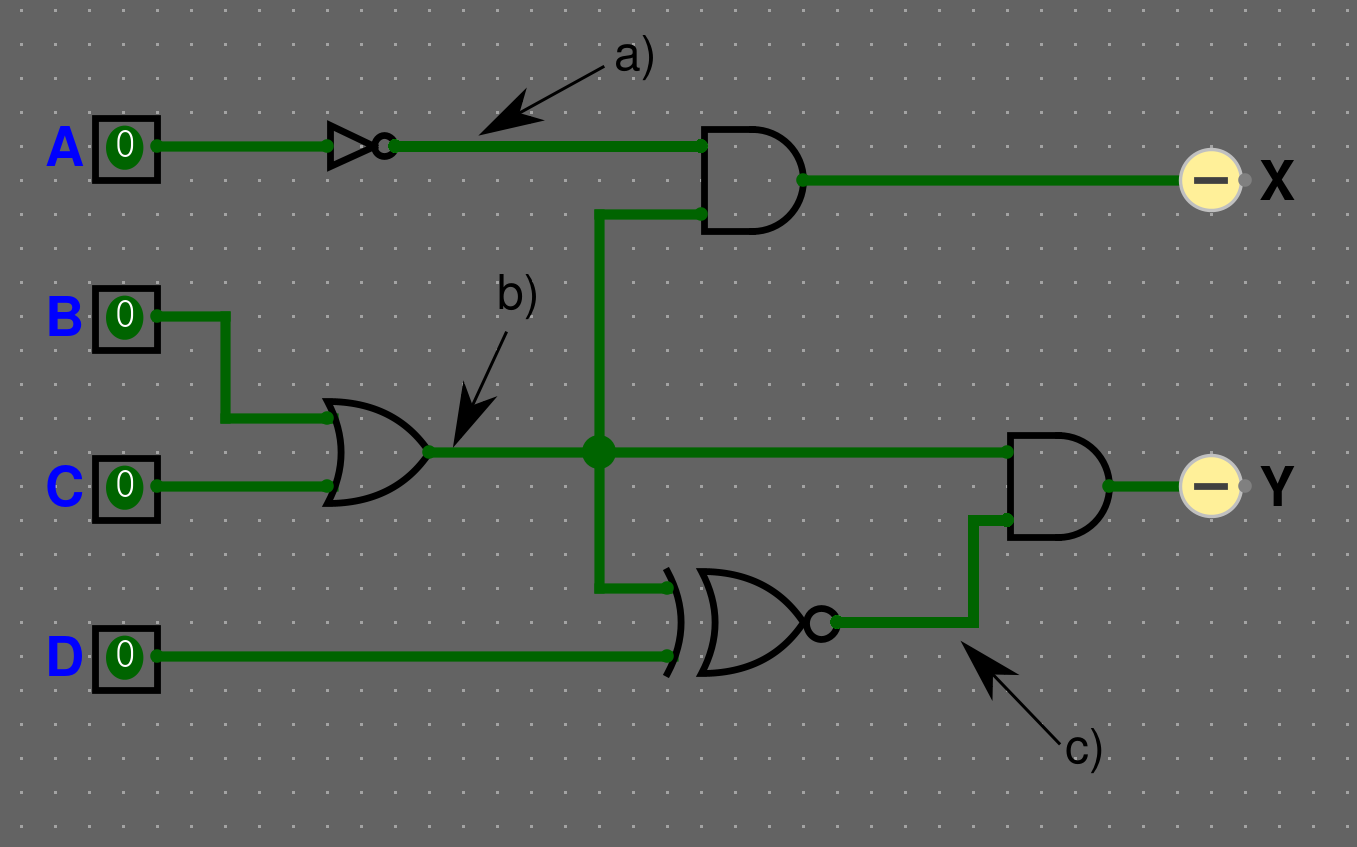
Řešení
a) \(\overline{A}\)
b) \(B+C\)
c) \(\overline{(B+C) \bigoplus D}\)
\(X = \overline{A} \cdot (B+C)\)
\(Y = (B+C) \cdot \overline{(B+C) \bigoplus D}\)
4. Nakresli zapojení pro následující výraz a nakresli pravdivostní tabulku
\(X = (A \cdot B) + (\overline{A \bigoplus C}) + \overline{B}\)
Řešení - zapojení
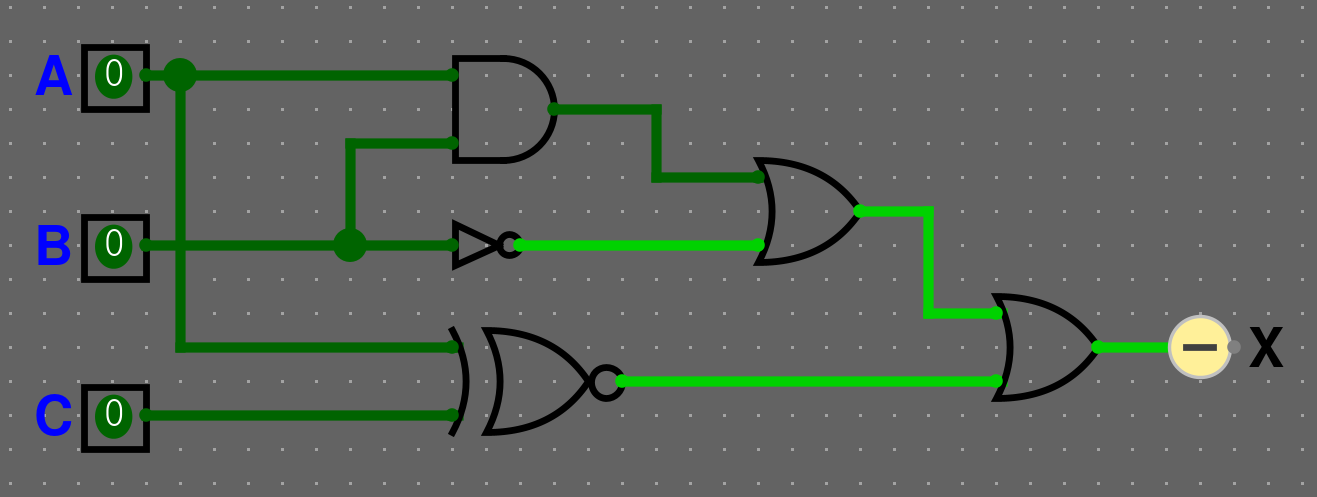
Řešení - tabulka
Taktéž v zapojení můžeme použít jeden OR, který příjmá 3 vstupy místo dvou (jelikož sčítání je asociativní a komutativní).
Vytváření tabulky si ulehčíme spočítáním sloupců pro námi zvolené podvýrazy (\(A \cdot B\), \(\overline{A \bigoplus C}\), \(\overline{B}\)) jejich hodnoty použijeme v dalších výpočtech, abychom se vyhnuli chybám při počítání komplikovaných výrazu z hlavy. Pokud víme na první pohled hodnoty některých řádků výsledku, můžeme je vyplnit hned do výsledku a v pomocných sloupcích je přeskočit. Nutné sloupce jsou pouze vstupy (\(A\),\(B\),\(C\)) a výstupy (\(X\)).
| \(A\) | \(B\) | \(C\) | \(A \cdot B\) | \(\overline{A \bigoplus C} \) | \(\overline{B}\) | \(X\) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
5. Zjednoduš následující výraz do co nejjednodušší podoby
Výsledek zde: \(\Box\)
\(X=(AC + C + B) + \overline{B \cdot \overline{C}} + \overline{C}(\overline{A}C +C)\)
Řešení
\(X = (C(A+1)+B)+\overline{B}+C+\overline{C}(C(\overline{A}+1))\)
\(X = (AC+B)+\overline{B} + C + \overline{C} \cdot (\overline{A}C)\)
\(X = AC + B + \overline{B} + C + 0\)
\(X = AC + 1 + C\)
\(X = 1\)
Výsledek zde: \(\Box + \Box\)
\(X=(A+C)(A \cdot B + \overline{\overline{A} + B}) + AC + C\)
Řešení
\(X = (A+C)(A \cdot B + A \cdot \overline{B}) + C\)
\(X = (A+C)(A \cdot (B+\overline{B})) + C\)
\(X = ((A+C) \cdot A) + C\)
\(X = A \cdot A + A \cdot C + C\)
\(X = A +C\)